【题目】如图1,在平面直角坐标系xOy中,点A( ![]() ,0),B(3
,0),B(3 ![]() ,0),以AB为直径的⊙G交y轴于C,D两点.
,0),以AB为直径的⊙G交y轴于C,D两点.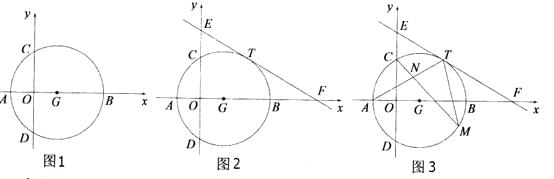
(1)填空:请直接写出⊙G的半径r,圆心G的坐标:r=;G( , ).
(2)如图2,直线y= ![]() 与x、y轴分别交于F、E两点,且经过圆上一点T(
与x、y轴分别交于F、E两点,且经过圆上一点T( ![]() ,m),求证:直线EF是⊙G的切线;
,m),求证:直线EF是⊙G的切线;
(3)在(2)的条件下,如图3,点M是⊙G优弧 ![]() 上的一个动点(不包括A、T两点),连接AT、CM、TM,CM交AT于点N,试问,是否存在一个常数k,始终满足CN·CM=k?如果存在,请求出k的值,如果不存在,请说明理由.
上的一个动点(不包括A、T两点),连接AT、CM、TM,CM交AT于点N,试问,是否存在一个常数k,始终满足CN·CM=k?如果存在,请求出k的值,如果不存在,请说明理由.
参考答案:
【答案】
(1)![]() ;
;![]() ;0
;0
(2)
解:如图,连接GT,过点T作TH⊥x轴于点H,直线y= ![]() 与x、y轴交于E、F两点,则易知:E(0,5),F(5
与x、y轴交于E、F两点,则易知:E(0,5),F(5 ![]() ,0),
,0),
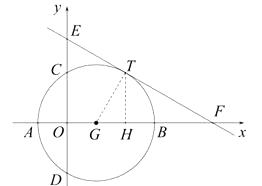
∵直线EF:y= ![]() 过点T(2
过点T(2 ![]() ,m),则
,m),则
m= ![]() +5=3,∴T(2
+5=3,∴T(2 ![]() ,3),
,3),
故TH=3,GH= ![]() ,HF=3
,HF=3 ![]() ,
,
在Rt△GHT中,有GT=r=2 ![]() ,
,
∴GH= ![]() GT,∴∠GTH=30°,
GT,∴∠GTH=30°,
在在Rt△THF中,有tan∠FTH= ![]() =
= ![]() ,∴∠FTH=60°,
,∴∠FTH=60°,
故∠GTF=∠GTH+∠FTH=30°+60°=90°,∴GT⊥EF,
∴直线EF是⊙G的切线.
(3)
解:存在.如图,连接 CG、CT、GT,在Rt△COG中,
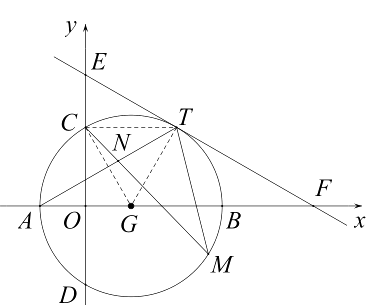
在Rt△COG中,OG= ![]() ,CG=r=2
,CG=r=2 ![]() ,
,
∴OC=3,∠CGO=60°,
由于C(0,3),T(2 ![]() ,3),故CT//x轴,
,3),故CT//x轴,
∴CT=2 ![]() ,
,
即CT=CG=GT=2 ![]() ,
,
∴△CGT是等边三角形,
∴∠CGT=∠TCG=∠CGA=60°,
∴∠CTA= ![]() ∠CGA=30°.
∠CGA=30°.
∴∠CTA=∠CMT,
在△CNT和△CTM中,∠TCA=∠MCT,∠CTN=∠CMT,
∴△CNT~△CTM,
∴ ![]() ,
,
∴CN·CM=CT2=(2 ![]() )2=12,
)2=12,
故存在一个常数12,始终范围CN·CM=12,即:k=12.
【解析】解:(1)∵A( ![]() ,0),B(3
,0),B(3 ![]() ,0),
,0),
∴AB=3 ![]() -(
-( ![]() )=4
)=4 ![]() ;
;
则r= ![]() AB=
AB= ![]() ,OG=
,OG= ![]() -
- ![]() =
= ![]() ,则G(
,则G( ![]() ,0).
,0).
【考点精析】本题主要考查了圆的定义和圆心角、弧、弦的关系的相关知识点,需要掌握平面上到定点的距离等于定长的所有点组成的图形叫做圆.定点称为圆心,定长称为半径;在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为降低空气污染,启东飞鹤公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年载客量如表:
A型
B型
价格(万元/台)
a
b
年载客量(万人/年)
60
100
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求a,b的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次.请你设计一个方案,使得购车总费用最少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形一腰上的高与另一腰的夹角是50°,则一个底角为______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某科技公司研发出一款多型号的智能手表,一家代理商出售该公司的A型智能手表去年销售总额为80000元,今年A型智能手表的售价每只比去年降低了600元,若售出的数量与去年相同,销售总额将比去年减少了25%.
(1)请问今年A型智能手表每只售价多少元?
(2)今年这家代理商准备新进一批A型智能手表和B型智能手表共100只,它们的进货价格与销售价格如表.若B型智能手表进货量不超过A型智能手表数量的3倍,所进智能手表可全部售完,请你设计出进货方案,使这批智能手表获利最多,并求出最大利润是多少元?A型智能手表
B型智能手表
进价
1300元/只
1500元/只
售价
今年的售价
2300元/只
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,∠5=∠CDA=∠ABC,∠1=∠4,∠2=∠3,∠BAD+∠CDA=180°,填空:

∵∠5=∠CDA(已知),∴________∥________(内错角相等,两直线平行).
∵∠5=∠ABC(已知),∴________∥________(同位角相等,两直线平行).
∵∠2=∠3(已知),∴________∥________(内错角相等,两直线平行).
∵∠BAD+∠CDA=180°(已知),
∴________∥________(同旁内角互补,两直线平行).
∵∠5=∠CDA(已知),
又∠5与∠BCD互补,
∠CDA与________互补,
∴∠BCD=∠6(等角的补角相等),
∴________∥________(同位角相等,两直线平行).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),B(4,0)两点,与y轴交于点C,且OC=3OA,点P是抛物线上的一个动点,过点P作PE⊥x轴于点E,交直线BC于点D,连接PC.
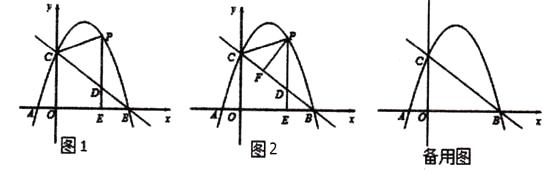
(1)试求抛物线的解析式;
(2)如图2,当动点P只在第一象限的抛物线上运动时,过点P作PF⊥BC于点F,试问△PFD的周长是否有最大值?如果有,请求出最大值;如果没有,请说明理由.
(3)当点P在抛物线上运动时,将△CPD沿直线CP翻折,点D的对应点为点Q,试问,四 边形CDPQ能否成为菱形?如果能,请求此时点P的坐标;如果不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在
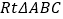 中,
中, 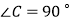 ,
, 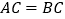 ,
, 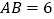 ,点
,点 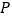 是
是 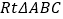 的重心,则点
的重心,则点 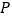 到
到 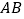 所在直线的距离等于( )
所在直线的距离等于( )
A.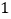
B.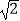
C.
D.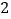
相关试题

