搜索
【题目】为了节省材料，某水产养殖户利用水库的岸堤（岸堤足够长）为一边，用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域，而且这三块矩形区域的面积相等．设BC的长度为xm，矩形区域ABCD的面积为ym2 ．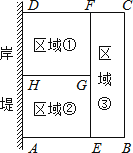 
（1）求y与x之间的函数关系式，并注明自变量x的取值范围；
（2）x为何值时，y有最大值？最大值是多少？
参考答案：
【答案】
（1）
解：∵三块矩形区域的面积相等，∴矩形AEFD面积是矩形BCFE面积的2倍，∴AE=2BE，设BE=a，则AE=2a，∴8a+2x=80，
∴a=﹣
x+10，3a=﹣
x+30，∴y=（﹣x+30）x=﹣x2+30x，∵a=﹣x+10＞0，∴x＜40，
则y=﹣x2+30x（0＜x＜40）；
（2）
解：∵y=﹣x2+30x=﹣（x﹣20）2+300（0＜x＜40），且二次项系数为﹣＜0，
∴当x=20时，y有最大值，最大值为300平方米．
【解析】根据三个矩形面积相等，得到矩形AEFD面积是矩形BCFE面积的2倍，可得出AE=2BE，设BE=a，则有AE=2a，表示出a与2a，进而表示出y与x的关系式，并求出x的范围即可。
利用二次函数的性质求出y的最大值，以及此时x的值即可．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算下面各题
（1）计算：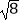
+（2011﹣ 
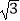）0﹣（ 
）﹣1
（2）计算：（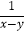
+ 
）÷ 
． -
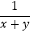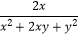科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠A=90°，O是BC边上一点，以O为圆心的半圆与AB边相切于点D，与AC、BC边分别交于点E、F、G，连接OD，已知BD=2，AE=3，tan∠BOD=
． 
（1）求⊙O的半径OD；
（2）求证：AE是⊙O的切线；
（3）求图中两部分阴影面积的和． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，O为坐标原点，抛物线y=
x2+2x与x轴相交于O、B，顶点为A，连接OA．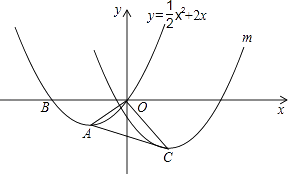
（1）求点A的坐标和∠AOB的度数；
（2）若将抛物线y= x2+2x向右平移4个单位，再向下平移2个单位，得到抛物线m，其顶点为点C．连接OC和AC，把△AOC沿OA翻折得到四边形ACOC′．试判断其形状，并说明理由；
（3）在（2）的情况下，判断点C′是否在抛物线y= x2+2x上，请说明理由．
（4）若点P为x轴上的一个动点，试探究在抛物线m上是否存在点Q，使以点O、P、C、Q为顶点的四边形是平行四边形，且OC为该四边形的一条边？若存在，请直接写出点Q的坐标；若不存在，请说明理由． （参考公式：二次函数y=ax2+bx+c（a≠0）图象的顶点坐标为（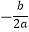
， 
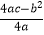），对称轴是直线x= ．） -
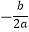科目： 来源： 题型：
查看答案和解析>>【题目】解下列各题
（1）解方程：
=1﹣ 
（2）解不等式组：
． -
科目： 来源： 题型：
查看答案和解析>>【题目】下面是某同学对多项式(a2－4a＋2)(a2－4a＋6)＋4进行因式分解的过程：
解：设a2－4a＝y，则
原式＝(y＋2)(y＋6)＋4(第一步)
＝y2＋8y＋16(第二步)
＝(y＋4)2(第三步)
＝(a2－4a＋4)2.(第四步)
(1)该同学因式分解的结果是否彻底：________(填“彻底”或“不彻底”)；
(2)若不彻底，请你直接写出因式分解的最后结果：________；
(3)请你模仿以上方法对多项式(x2－2x)(x2－2x＋2)＋1进行因式分解．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某厂家在甲、乙两家商场销售同一商品所获利润分别为y甲，y乙（单位：元），y甲，y乙与销售数量x（单位：件）的函数关系如图所示，请根据图象解决下列问题：
（1）分别求出y甲，y乙与x的函数关系式；
（2）现厂家分配该商品给甲、乙两商场共计1200件，当甲、乙商场售完这批商品，厂家可获得总利润为1080元，问厂家如何分配这批商品？
相关试题
