【题目】如图,△ABC中,∠A=67.5°,BC=4,BE⊥CA于E,CF⊥AB于F,D是BC的中点.以F为原点,FD所在直线为x轴构造平面直角坐标系,则点E的坐标是__________.

参考答案:
【答案】(2-![]() ,
,![]() )
)
【解析】分析:连接DE,过E作EH⊥OD于H,求得∠EDO=45°,即可得到Rt△DEH中,DH=cos45°×DE=![]() ,EH=
,EH=![]() ,进而得出OH=OD-DH=2-
,进而得出OH=OD-DH=2-![]() ,即点E的坐标是(2-
,即点E的坐标是(2-![]() ,
,![]() ).
).
详解:如图所示,连接DE,过E作EH⊥OD于H,
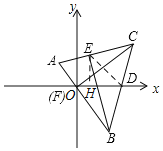
∵BE⊥CA于E,CF⊥AB于F,D是BC的中点,
∴DE=DC=![]() BC=DO=DB=2,
BC=DO=DB=2,
∴∠DCE=∠DEC,∠DBO=∠DOB,
∵∠A=67.5°,
∴∠ACB+∠ABC=112.5°,
∴∠CDE+∠BDO=(180°-2∠DCE)+(180°-2∠DBO)
=360°-2(∠DCE+∠DBO)
=360°-2×112.5°
=135°,
∴∠EDO=45°,
∴Rt△DEH中,DH=cos45°×DE=![]() ,EH=
,EH=![]()
∴OH=OD-DH=2-![]() ,
,
点E的坐标是(2-![]() ,
,![]() )
)
故答案为:(2-![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节约意识,我市出台阶梯电价计算方案如下表:
价目表
不超过
 度的部分
度的部分 元/度
元/度超过
 度不超过
度不超过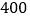 度的部分
度的部分 元/度
元/度超过
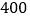 度的部分
度的部分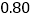 元/度
元/度注:电费按月结算
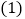 某户居民
某户居民 月份应缴电费
月份应缴电费 元,该户居民
元,该户居民 月份用电多少度?
月份用电多少度? 某户居民
某户居民 月份用电
月份用电 度,应缴电费
度,应缴电费 元,求
元,求 的值;
的值; 用
用 (度)表示月用电量,请根据
(度)表示月用电量,请根据 的不同取值范围用含
的不同取值范围用含 的代数式表示该月应缴电费.
的代数式表示该月应缴电费. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、CD分别表示两幢相距36米的大楼,高兴同学站在CD大楼的P处窗口观察AB大楼的底部B点的俯角为45°,观察AB大楼的顶部A点的仰角为30°,求大楼AB的高.

-
科目: 来源: 题型:
查看答案和解析>>【题目】直线l:y=﹣
 x+6交y轴于点A,与x轴交于点B,过A、B两点的抛物线m与x轴的另一个交点为C,(C在B的左边),如果BC=5,求抛物线m的解析式,并根据函数图像指出当m的函数值大于0的函数值时x的取值范围.
x+6交y轴于点A,与x轴交于点B,过A、B两点的抛物线m与x轴的另一个交点为C,(C在B的左边),如果BC=5,求抛物线m的解析式,并根据函数图像指出当m的函数值大于0的函数值时x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是正方形ABCD的对角线AC上的一个动点(不与A、C重合),作EF⊥AC交边BC于点F,联结AF、BE交于点G.

(1)求证:△CAF∽△CBE;
(2)若AE:EC=2:1,求tan∠BEF的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(能简便的用简便方法计算)
(1)8+(-10)-(-5) (2)

(3)
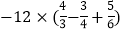 (4)
(4)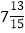 ×(-30)
×(-30)(5)
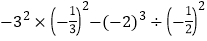
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2﹣
 x+2(a≠0)的图像与x轴交于A、B两点,与y轴交于点C,已知点A(﹣4,0).
x+2(a≠0)的图像与x轴交于A、B两点,与y轴交于点C,已知点A(﹣4,0). 
(1)求抛物线与直线AC的函数解析式;
(2)若点D(m,n)是抛物线在第二象限的部分上的一动点,四边形OCDA的面积为S,求S关于m的函数关系;
(3)若点E为抛物线上任意一点,点F为x轴上任意一点,当以A、C、E、F为顶点的四边形是平行四边形时,请直接写出满足条件的所有点E的坐标.
相关试题

