【题目】一个大矩形按如图方式分割成九个小矩形,且只有标号为①和②的两个小矩形为正方形.在满足条件的所有分割中,若知道九个小矩形中n个小矩形的周长,就一定能算出这个在大矩形的面积,则n的最小值是 ( )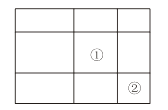
A.3
B.4
C.5
D.6
参考答案:
【答案】A
【解析】解:要算出这个在大矩形的面积,就需要知道大矩形的长和宽.
如图: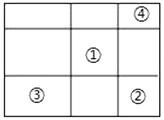
假设已知小矩形①的周长为4x,小矩形③周长为2y,小矩形④周长为2z;
则可得出①的边长以及③和④的邻边和,分别为x、y、z;
设小矩形②的周长为4a,则②的边长为a,可得③、④都有一边长为a
则③和④的另一条边长分别为:y﹣a,z﹣a,
故大矩形的边长分别为:y﹣a+x+a=y+x,z﹣a+x+a=z+x,
故大矩形的面积为:(y+x)(z+x),当x,y,z都为已知数时,即可算出大正方形的面积,
故n的最小值是3.
故选:A.
【考点精析】通过灵活运用推理与论证,掌握一个正确的论证必须满足两个条件:1、论据(前提)是真实的;2、论证方式(推理形式)是正确的(有效的)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
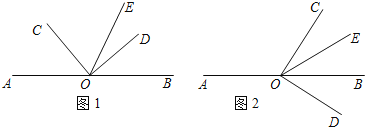
(1)如图(1),若∠AOC=
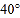 ,求∠DOE的度数;
,求∠DOE的度数;(2)如图(2),将∠COD绕顶点O旋转,且保持射线OC在直线AB上方,在整个旋转过程中,当∠AOC的度数是多少时,∠COE=2∠DOB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4)与x轴交于点A、B,点B(4,0),抛物线的对称轴为x=1.直线AD交抛物线于点D(2,m).
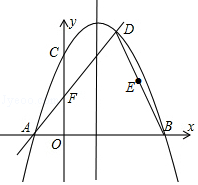
(1)求二次函数的解析式并写出D点坐标;
(2)点E是BD的中点,点Q是线段AB上一动点,当△QBE和△ABD相似时,求点Q的坐标;
(3)抛物线与y轴交于点C,直线AD与y轴交于点F,点M为抛物线对称轴上的动点,点N在x轴上,当四边形CMNF周长取最小值时,求出满足条件的点M和点N的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上的点A,B对应的数分别是x,y,且|x+100|+(y﹣200)2=0,点P为数轴上从原点出发的一个动点,速度为30单位长度/秒.
(1)求点A,B两点之间的距离;
(2)若点A向右运动,速度为10单位长度/秒,点B向左运动,速度为20单位长度/秒,点A,B和P三点同时开始运动,点P先向右运动,遇到点B后立即掉后向左运动,遇到点A再立即掉头向右运动,如此往返,当A,B两点相距30个单位长度时,点P立即停止运动,求此时点P移动的路程为多少个单位长度?
(3)若点A,B,P三个点都向右运动,点A,B的速度分别为10单位长度/秒,20单位长度/秒,点M、N分别是AP、OB的中点,设运动的时间为t(0<t<10),在运动过程中①
 的值不变;②
的值不变;②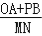 的值不变,可以证明,只有一个结论是正确的,请你找出正确的结论并求值.
的值不变,可以证明,只有一个结论是正确的,请你找出正确的结论并求值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某年的日历表,在此日历表上可以用一个矩形圈出3×3个位置的9个数(如3,4,5,10,11,12,17,18,19).若用这样的矩形圈圈这张日历表的9个数,则圈出的9个数的和不可能为下列数中的( )

A. 81 B. 90 C. 108 D. 216
-
科目: 来源: 题型:
查看答案和解析>>【题目】华联超市用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的
 多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)甲
乙
进价(元/件)
22
30
售价(元/件)
29
40
(1)该商场购进甲、乙两种商品各多少件?
(2)该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.

相关试题

