【题目】一副三角板的三个内角分别是90°,45°,45°和90°,60°,30°,按如图所示叠放在一起,若固定三角形AOB,改变三角形ACD的位置(其中点A位置始终不变),可以摆成不同的位置,使两块三角板至少有一组边平行.设∠BAD=α(0°<α<180°)
(1)如图2中,请你探索当α为多少时,CD∥OB,并说明理由;
(2)如图3中,当α=时,AD∥OB;
(3)在点A位置始终不变的情况下,你还能摆成几种不同的位置,使两块三角板中至少有一组边平行,请直接写出符合要求的α的度数.
参考答案:
【答案】
(1)
解:如图2,
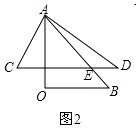
∵CD∥OB,
∴∠AEC=∠B=45°,
∵∠D=30°,
∴α=∠BAD=45°﹣30°=15°,
∴当α=15°时,CD∥OB
(2)45°
(3)
解:①如图4,
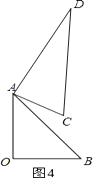
∵CD∥OA,
∴∠D+∠DAO=180,
∴∠BAD=180°﹣45°﹣30°=105°,
∴当α=105°时,CD∥OA;
②如图5,
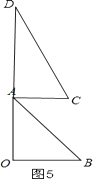
∵AC∥OB,
∴∠CAB=∠B=45°,
∴∠BAD=∠CAB+∠CAD=45°+90°=135°,
∴当α=135°时,AC∥OB;
③如图6,
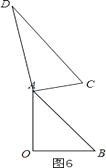
∵DC∥AB,
∴∠C=∠BAC=60,
∴∠BAD=90°+60°=150°,
∴当α=150°时,DC∥AB;
④如图7,连接BC,

∵DC∥OB,
∴∠DCB+∠OBC=180°,
∵∠ACD=60°,∠OBA=45°,
∴∠ACB+∠ABC=180°﹣60°﹣45°=75°,
∴∠CAB=105°,
∴∠BAD=360°﹣90°﹣105°=165°,
∴当α=165°时,CD∥OB;
⑤如图8,
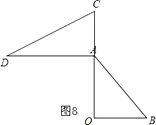
∵AD∥OB,
∴∠DAO=∠O=90°,
∴∠BAD=90°+45°=135°,
∴当α=135°时,AD∥OB;
⑥如图9,

∵CD∥OA,
∴∠D=∠DAO=30°,
∴∠BAD=30°+45°=75°,
∴当α=75°时,CD∥OA;
⑦如图10,
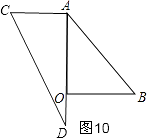
∵AC∥OB,
∴AO与AD重合,
∴∠BAD=45°,
∴当α=45°时,AC∥OB;
⑧如图11,
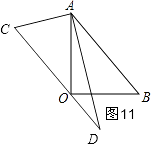
∵OC∥AB,
∴∠BAD=∠D=30°,
∴当α=30°时,OC∥AB.
【解析】解:(2)如图3,∵AD∥OB,
∴∠BAD=∠B=45°,
∴当α=45°时,AD∥OB,
所以答案是:45°;
【考点精析】利用同位角、内错角、同旁内角对题目进行判断即可得到答案,需要熟知两条直线被第三条直线所截形成八个角,它们构成了同位角、内错角与同旁内角;判别同位角、内错角或同旁内角的关键是找到构成这两个角的“三线”,有时需要将有关的部分“抽出”或把无关的线略去不看,有时又需要把图形补全.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在解一元二次方程时,他是这样做的:
解一元二次方程
3x2﹣8x(x﹣2)=0…第一步
3x﹣8x﹣2=0…第二步
﹣5x﹣2=0…第三步
﹣5x=2…第四步
x=﹣
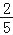 …第五步
…第五步 (1)小明的解法从第 步开始出现错误;此题的正确结果是 .
(2)用因式分解法解方程:x(2x﹣1)=3(2x﹣1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式: (x﹣1)(x+1)=x2﹣1
(x﹣1)(x2+x+1)=x3﹣1
(x﹣1)(x3+x2+x+1)=x4﹣1
(1)根据各式的规律,可推测: (x﹣1)(xn﹣1+xn﹣2+…+x+1)=
(2)根据你的结论计算: 1+2+22+23+…+22013+22014
(3)1+3+32+33+…+32013+32014的个位数字是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】选用合适的方法解下列方程
(1)(x+4)2=5(x+4);(2)(x+3)2=(1﹣2x)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°,则下列结论正确的有( ) (1.)∠C′EF=32°(2.)∠AEC=116°(3.)∠BGE=64° (4.)∠BFD=116°.

A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】单项式﹣2xy2z3的系数和次数是( )
A.2,6
B.﹣2,6
C.﹣2,5
D.﹣2,3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b互为相反数,c,d互为倒数,则a+b+cd=_____.
相关试题

