Question

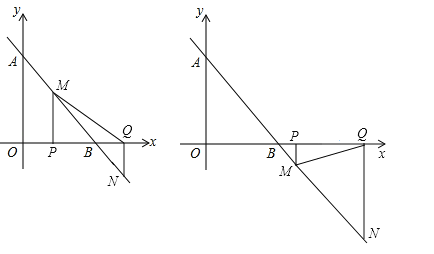
【题目】如图，在平面直角坐标系中，一次函数y=kx+b的图象与y轴的正半轴交于点A，与x轴交于点B（2，0），三角形△ABO的面积为2．动点P从点O出发，以每秒1个单位长度的速度在射线OB上运动，动点Q从B出发，沿x轴的正半轴与点P同时以相同的速度运动，过P作PM⊥X轴交直线AB于M．

（1）求直线AB的解析式．

（2）当点P在运动时，设△MPQ的面积为S，点P运动的时间为t秒，求S与t的函数关系式（直接写出自变量的取值范围）．

（3）过点Q作QN⊥X轴交直线AB于N，在运动过程中（P不与B重合），是否存在某一时刻t（秒），使△MNQ是等腰三角形？若存在，求出时间t值．

Answer 1

【答案】（1）直线AB的解析式为y=﹣x+2；（2）t=或4时，△MNQ是等腰三角形．

【解析】试题分析：（1）根据三角形的面积求出OA，再写出点A的坐标，然后利用待定系数法求一次函数解析式解答；

（2）根据等腰直角三角形的性质表示出PM，再求出PQ的长，然后利用直角三角形的面积公式列式整理即可得解；

（3）表示出PM、QN，再利用勾股定理列式表示出QM2，再求出MN，然后分MN=QN，MN=QM，QN=QM三种情况列出方程求解即可．

试题解析：解：（1）∵点B（2，0），∴OB=2，∴S△ABO=OBOA=×2OA=2，解得OA=2，∴点A（0，2），设直线AB的解析式为y=kx+b，则： ，解得： ，∴直线AB的解析式为y=﹣x+2；

（2）∵OA=OB=2，∴△ABO是等腰直角三角形，∵点P、Q的速度都是每秒1个单位长度，∴PM=PB=OB﹣OP=2﹣t，PQ=OB=2，∴△MPQ的面积为S=PQPM=×2×（2﹣t）=2﹣t，∵点P在线段OB上运动，∴0＜t＜2，∴S与t的函数关系式为S=2﹣t（0＜t＜2）；

（3）t秒时，PM=PB=|2﹣t|，QN=BQ=t，所以，QM2=PM2+PQ2=（2﹣t）2+4，MN=（QN﹣PM）=（t﹣t﹣2）=．

①若MN=QN，则t=；

②若MN=QM，则（2﹣t）2+4=（）2，整理得，t2﹣4t=0，解得t1=0（舍去），t2=4；

③若QN=QM，则（2﹣t）2+4=t2，理得，4t﹣8=0，解得t=2，此时点P在与点B重合，不合题意舍去．

综上所述，t=或4时，△MNQ是等腰三角形．