【题目】如图,在△ABC中,∠B![]() 90°,AB
90°,AB![]() 4,BC
4,BC![]() 2,以AC为边作△ACE,∠ACE
2,以AC为边作△ACE,∠ACE![]() 90°,AC=CE,延长BC至点D,使CD
90°,AC=CE,延长BC至点D,使CD![]() 5,连接DE.求证:△ABC∽△CED.
5,连接DE.求证:△ABC∽△CED.

参考答案:
【答案】证明见解析
【解析】试题分析:
由已知易证∠BAC=∠ECD,在Rt△ABC中由已知可得AC=![]() =CE, 结合AB=4,CD=5,可证得
=CE, 结合AB=4,CD=5,可证得![]() ,由此即可由“两边对应成比例,且夹角相等的两三角形相似”得到△ABC∽△CED.
,由此即可由“两边对应成比例,且夹角相等的两三角形相似”得到△ABC∽△CED.
试题解析:
∵ ∠B=90°,AB=4,BC=2,
∴![]() .
.
∵ CE=AC,
∴![]() .
.
∵ CD=5,
∴![]() .
.
∵ ∠B=90°,∠ACE=90°,
∴ ∠BAC+∠BCA=90°,∠BCA+∠DCE=90°.
∴ ∠BAC=∠DCE.
∴ △ABC∽△CED.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简(1)

(2)
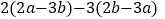
(3)已知
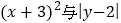 互为相反数,
互为相反数, 是绝对值最小的有理数,求
是绝对值最小的有理数,求 的值.
的值.(4)先化简,再求值:
 ,其中
,其中 、
、 满足
满足 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是“作一个30°角”的尺规作图过程.

请回答:该尺规作图的依据是______________________________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲.乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离S(km)和骑行时间t(h)之间的函数关系如图1所示,给出下列说法:①他们都骑行了20km;②乙在途中停留了0.5h;③甲.乙两人同时到达目的地;④相遇后,甲的速度小于乙的速度.
根据图象信息,以上说法正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 分别与x轴、y轴交于
分别与x轴、y轴交于 两点,与直线
两点,与直线 交于点C(4,2).
交于点C(4,2).(1)点A坐标为( , ),B为( , );
(2)在线段
 上有一点E,过点E作y轴的平行线交直线
上有一点E,过点E作y轴的平行线交直线 于点F,设点E的横坐标为m,当m为何值时,四边形
于点F,设点E的横坐标为m,当m为何值时,四边形 是平行四边形;
是平行四边形;(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得
 四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】古代阿拉伯数学家泰比特·伊本·奎拉对勾股定理进行了推广研究:如图(图1中
 为锐角,图2中
为锐角,图2中 为直角,图3中
为直角,图3中 为钝角).
为钝角).
在△ABC的边BC上取
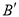 ,
,  两点,使
两点,使 ,则
,则 ∽
∽ ∽
∽ ,
,  ,
, 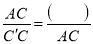 ,进而可得
,进而可得
 ;(用
;(用 表示)
表示)若AB=4,AC=3,BC=6,则

 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数
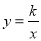 (x<0)与y=ax+b的图象交于点A(﹣1,n)和点B(﹣2,1).
(x<0)与y=ax+b的图象交于点A(﹣1,n)和点B(﹣2,1).(1)求k,a,b的值;
(2)直线x=m与
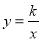 (x<0)的图象交于点P,与y=﹣x+1的图象交于点Q,当∠PAQ>90°时,直接写出m的取值范围.
(x<0)的图象交于点P,与y=﹣x+1的图象交于点Q,当∠PAQ>90°时,直接写出m的取值范围.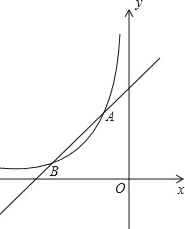
相关试题

