【题目】疫情期间,为满足口罩需求,某商店决定购进A,B两种口罩。若购进A口罩10盒,B口罩5盒,需要1000元。若购进A口罩4盒,B口罩3盒,需要550元.
(1)求A,B两种口罩每盒需要多少元?
(2)若该商店决定拿出10000元全部用来购进这两种口罩,考虑到市场需求,要求购进A口罩的数量不少于B口罩数量的6倍,且不超过B口罩数量的8倍,那么该商店共有几种进货方案?
(3)若销售每盒A口罩可以获利润20元,每盒B口罩可以获利润30元,在(2)的各种进货方案中,哪种方案获利最大?最大利润是多少元?
参考答案:
【答案】(1)某商店购进A种口罩每盒需25元,购进B种口罩每盒需150元;(2)该商店共有5种进货方案;(3)销售A种口罩226盒,B种口罩29盒方案获利最大,最大利润是5390元.
【解析】
(1)设某商店购进A种口罩每盒需a元,购进B种口罩每盒需b元,根据条件建立二元一次方程组求出其解即可;
(2)设某商店购进A种口罩x盒,购进B种口罩y盒,根据条件的数量关系建立不等式组求出其解即可;
(3)根据总利润=两种商品的利润之和,列出算式计算就可以求出结论.
解:(1)设某商店购进A种口罩每盒需a元,购进B种口罩每盒需b元,则
![]() ,
,
解得:![]() ,
,
答:某商店购进A种口罩每盒需25元,购进B种口罩每盒需150元.
(2)设某商店购进A种口罩x盒,购进B种口罩y盒,则
![]() ,
,
解得:![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∵![]() 为整数,
为整数,
∴y=29,30,31,32,33,
∴![]() 226,220,214,208,202;
226,220,214,208,202;
答:该商店共有5种进货方案;
(3)方案1购买A中口罩226盒,B中口罩29盒,
利润为:226×20+29×30=5390(元);
方案2购买A中口罩220盒,B中口罩30盒,
利润为:220×20+30×30=5300(元);
方案3购买A中口罩214盒,B中口罩31盒,
利润为:214×20+30×31=5210(元);
方案4购买A中口罩208盒,B中口罩32盒,
利润为:208×20+30×32=5120(元);
方案5购买A中口罩202盒,B中口罩33盒,
利润为:202×20+30×33=5030(元).
答:销售A种口罩226盒,B种口罩29盒方案获利最大,最大利润是5390元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某人去水果批发市场采购猕猴桃,他看中了A、B两家猕猴桃.这两家猕猴桃品质一样,零售价都为6元/千克,批发价各不相同,
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠.
B家的规定如下表:
数量范围
(千克)
0~500
500以上~1500
1500以上~2500
2500以上
价格(元)
零售价的95%
零售价的85%
零售价的75%
零售价的70%
(1)如果他批发600千克猕猴桃,则他在A 、B两家批发分别需要多少元?
(2)如果他批发x千克猕猴桃(1500<x<2000),请你分别用含x的代数式表示他在A、B两家批发所需的费用;
(3)现在他要批发1800千克猕猴桃,你能帮助他选择在哪家批发更优惠吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
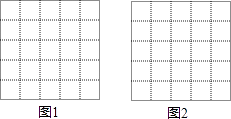
(1)在图1中画出钝角△ABC,使它的面积为6(画一个即可);
(2)在图2中画出△DEF,使它的三边长分别为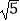 、2
、2 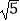 、5(画一个即可).并且直接写出此时三角形DEF的面积.
、5(画一个即可).并且直接写出此时三角形DEF的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明在某商店购买商品A,B共3次,只有一次购买时,商品同时打折,其余两次均按标价购买,三次购买商品A,B的数量和费用如下表:
购买商品A的数量(个)
购买商品B的数量(个)
购买总费用(元)
第一次购买
7
6
1350
第二次购买
4
8
1320
第三次购买
10
9
1188
(1)小明以折扣价购买商品的是第_____次购物;
(2)求商品A,B的标价;
(3)若商品A,B的折扣相同,问商店是打几折出售的这两种商品.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁一起研究一道数学题,如图,已知 EF⊥AB,CD⊥AB,甲说:“如果还知道∠CDG=∠BFE,则能得到∠AGD=∠ACB.”乙说:“如果还知道∠AGD=∠ACB,则能得到∠CDG=∠BFE.”丙说:“∠AGD 一定大于∠BFE.”丁说:“如果连接 GF,则 GF∥AB.”他们四人中,正确的是( )
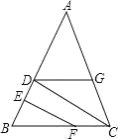
A.0 个B.1 个C.2 个D.3 个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在Rt△ABC中,∠ACB=90°,现按如下步骤作图:
①分别以A,C为圆心,a为半径(a>
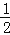 AC)作弧,两弧分别交于M,N两点;
AC)作弧,两弧分别交于M,N两点;②过M,N两点作直线MN交AB于点D,交AC于点E;
③将△ADE绕点E顺时针旋转180°,设点D的像为点F.

(1)请在图中直线标出点F并连接CF;
(2)求证:四边形BCFD是平行四边形;
(3)当∠B为多少度时,四边形BCFD是菱形.
-
科目: 来源: 题型:
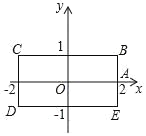
查看答案和解析>>【题目】如图,长方形 BCDE 的各边分别平行于 x 轴或 y 轴,物体甲和物体乙分别由点 A(2,0)同时出发,沿长方形 BCDE 的边作环绕运动,物体甲按逆时针方向以 1 个单位/秒匀速运动,物体乙按顺时针方向以 2 个单位/秒匀速运动,则两个物体运动后的第 2020 次相遇地点的坐标是_____.
相关试题

