【题目】已知:![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 内一点,连接
内一点,连接![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.


(1)如图1,求证:![]() ;
;
(2)如图2,点![]() 为
为![]() 的中点,分别连接
的中点,分别连接![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(3)如图3,在(2)的条件下,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,若
,若![]() ,
,![]() 的面积为30,
的面积为30,![]() ,求线段
,求线段![]() 的长.
的长.
参考答案:
【答案】(1)见解析;(2)45°;(3)10![]()
【解析】
(1)根据全等三角形的判定得出△CAE≌△ABD,进而利用全等三角形的性质得出AE=BD;
(2)根据全等三角形的判定得出△AEH≌△BDH,进而利用全等三角形的性质解答;
(3)过点M作MS⊥FH于点S,过点E作ER⊥FH,交HF的延长线于点R,过点E作ET∥BC,根据全等三角形判定和性质解答即可.
证明:(1)∵CE⊥AE,BD⊥AE,
∴∠AEC=∠ADB=90°,
∵∠BAC=90°,
∴∠ACE+CAE=∠CAE+∠BAD=90°,
∴∠ACE=∠BAD,
在△CAE与△ABD中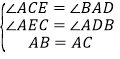
∴△CAE≌△ABD(AAS),
∴AE=BD;
(2)连接AH,如图2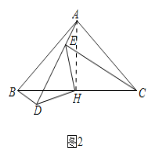
∵AB=AC,BH=CH,![]() ,
,
∴∠BAH=![]() ∠BAC=
∠BAC=![]() ×90°=45°,∠AHB=90°,
×90°=45°,∠AHB=90°,
∴∠ABH=∠BAH=45°,
∴AH=BH,
∵∠EAH=∠BAH-∠BAD=45°-∠BAD,
∠DBH=180°-∠ADB-∠BAD-∠ABH=45°-∠BAD,
∴∠EAH=∠DBH,
在△AEH与△BDH中 ∴△AEH≌△BDH(SAS),
∴△AEH≌△BDH(SAS),
∴EH=DH,∠AHE=∠BHD,
∴∠AHE+∠EHB=∠BHD+∠EHB=90°
即∠EHD=90°,
∴∠EDH=∠DEH=![]() =45°
=45°
(3)过点M作MS⊥FH于点S,过点E作ER⊥FH,交HF的延长线于点R,过点E作ET∥BC,交HR的延长线于点T.如图3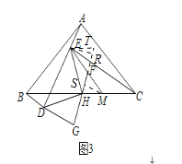
∵DG⊥FH,ER⊥FH,
∴∠DGH=∠ERH=90°,
∴∠HDG+∠DHG=90°
∵∠DHE=90°,
∴∠EHR+∠DHG=90°,
∴∠HDG=∠HER
在△DHG与△HER中
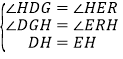 ∴△DHG≌△HER(AAS),
∴△DHG≌△HER(AAS),
∴HG=ER,
∵ET∥BC,
∴∠ETF=∠BHG,∠EHB=∠HET,
∴∠ETF=∠FHM,
∵∠EHB=∠BHG,
∴∠HET=∠ETF,
∴HE=HT,
在△EFT与△MFH中
 ,
,
∴△EFT≌△MFH(AAS),
∴HF=FT,
∵![]() =
=![]() ,
,
∴ER=MS,
∴HG=ER=MS,
设GH=6k,FH=5k,则HG=ER=MS=6k,
∴![]() ==30,
==30,
∴k=![]() ,
,
∴FH=5![]() ,
,
∴HE=HT=2HF=10![]() ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠3,∠2+∠3=180,请说明AB与DE平行的理由.
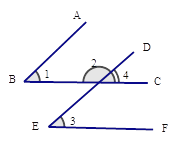
解:将∠2的邻补角记作∠4,则
∠2+∠4=180°( )
因为∠2+∠3=180°( )
所以∠3=∠4( )
因为______________(已知)
所以∠1=∠4( )
所以AB//DE( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】张师傅开车到某地送货,汽车出发前油箱中有油50升,行驶一段时间,张师傅在加油站加油,然后继续向目的地行驶.已知加油前、后汽车都匀速行驶,汽车行驶时每小时的耗油量一定.油箱中剩余油量Q(升)与汽车行驶时间t(时)之间的函数图象如图所示.
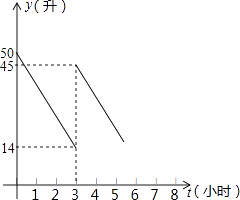
(1)张师傅开车行驶小时后开始加油,本次加油升.
(2)求加油前Q与t之间的函数关系式.
(3)如果加油站距目的地210千米,汽车行驶速度为70千米/时,张师傅要想到达目的地,油箱中的油是否够用?请通过计算说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:在三角形中,把一边的中点到这条边的高线的距离叫做这条边的中垂距.
例:如图①,在△ABC中,D为边BC的中点,AE⊥BC于E,则线段DE的长叫做边BC的中垂距.
(1)设三角形一边的中垂距为d(d≥0).若d=0,则这样的三角形一定是 , 推断的数学依据是 .
(2)如图②,在△ABC中,∠B=45°,AB= ,BC=8,AD为边BC的中线,求边BC的中垂距.
,BC=8,AD为边BC的中线,求边BC的中垂距.
(3)如图③,在矩形ABCD中,AB=6,AD=4.点E为边CD的中点,连结AE并延长交BC的延长线于点F,连结AC.求△ACF中边AF的中垂距.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,AB=BC=6,∠B=60°,∠D=90°,连结AC.动点P从点B出发,沿BC以每秒1个单位的速度向终点C运动(点P不与点B、C重合).过点P作PQ⊥BC交AB或AC于点Q,以PQ为斜边作Rt△PQR,使PR∥AB.设点P的运动时间为t秒.

(1)当点Q在线段AB上时,求线段PQ的长.(用含t的代数式表示)
(2)当点R落在线段AC上时,求t的值.
(3)设△PQR与△ABC重叠部分图形的面积为S平方单位,求S与t之间的函数关系式.
(4)当点R到C、D两点的距离相等时,直接写出t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD、EF被直线GH所截,已知AB//CD,∠1+∠2=180°,请填写CD//EF的理由.
解:因为∠1=∠3( )
_____________________(已知)
所以∠2+∠3=180°( )
得AB//EF( )
因为AB//CD( )
所以CD//EF( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣x+3与抛物线
 交于A、B两点,点A在x轴上,点B的横坐标为
交于A、B两点,点A在x轴上,点B的横坐标为  .动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
.动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
(1)求b、c的值.
(2)当点N落在直线AB上时,直接写出m的取值范围.
(3)当点P在A、B两点之间的抛物线上运动时,设正方形PQMN的周长为C,求C与m之间的函数关系式,并写出C随m增大而增大时m的取值范围.
(4)当△PQM与坐标轴有2个公共点时,直接写出m的取值范围.
相关试题

