搜索
【题目】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DF
(1)求∠CDE的度数
(2)求证:DF是⊙O的切线
参考答案：
【答案】证明见解析
【解析】试题分析：（1）直接利用圆周角定理得出∠CDE的度数；
（2）直接利用直角三角形的性质结合等腰三角形的性质得出∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°，进而得出答案.
试题解析：（1）∵对角线AC为⊙O的直径，
∴∠ADC=90°，
∴∠EDC=90°；
（2）连接DO，
∵∠EDC=90°，F是EC的中点，∴DF=FC，
∴∠FDC=∠FCD，
∵OD=OC ，∴∠OCD=∠ODC，
∵∠OCF=90°，∴∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°，
∴DF是⊙O的切线.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线AB∥CD，直线l与直线AB，CD相交于点E，F，点P是射线EA上的一个动点（不包括端点E），将△EPF沿PF折叠，使顶点E落在点Q处．
⑴若∠PEF＝48°,点Q恰好落在其中的一条平行线上,则∠EFP的度数为 ．
⑵若∠PEF＝75°，∠CFQ＝
∠PFC，求∠EFP的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小亮从家步行到公交车站台，等公交车去学校. 图中的折线表示小亮的行程s(km)与所花时间t(min)之间的函数关系. 下列说法错误的是
A. 他离家8km共用了30min B. 他等公交车时间为6min
C. 他步行的速度是100m/min D. 公交车的速度是350m/min
-
科目： 来源： 题型：
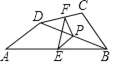
查看答案和解析>>【题目】如图，在四边形ABCD中，点P是对角线BD的中点，点E、F分别是AB、CD的中点，AD＝BC，且∠A+∠ABC＝90°，则∠PEF＝_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】弹簧挂上物体后会伸长，（在弹性限度
内）已知一弹簧的长度
与所挂物体的质量
之间的关系如下表：物体的质量
0
1
2
3
4
5
弹簧的长度
12
12.5
13
13.5
14
14.5
（1）当物体的质量为
时，弹簧的长度是多少？（2）如果物体的质量为
，弹簧的长度为
，根据上表写出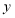
与x的关系式；（3）当物体的质量为
时，求弹簧的长度． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，每个小正方形的边长为1cm
（1）求四边形ABCD的面积；
（2）四边形ABCD中有直角吗？若有，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】网店店主小李进了一批某种商品，每件进价10元.预售一段时间后发现：每天销售量
（件）与售价
（元/件）之间成一次函数关系：
.（1）小李想每天赚取利润150元，又要使所进的货尽快脱手，则售价定为多少合适？
（2）小李想每天赚取利润300元，这个想法能实现吗？为什么？
相关试题
