【题目】如图,已知![]() ,
,![]() 于
于![]() ,
,![]() 为
为![]() 中点,连接
中点,连接![]() ,将
,将![]() 向右平移到
向右平移到![]() ,使
,使![]() 与
与![]() 重合,
重合,![]() 与
与![]() 重合,
重合,![]() 与
与![]() 重合,连接
重合,连接![]() ,
,![]() ,
,![]() ,若
,若![]() 为
为![]() 的高的交点,
的高的交点,![]() ,
,![]() ,则
,则![]() 到
到![]() 的距离为________.
的距离为________.
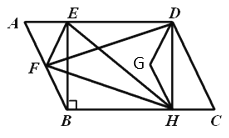
参考答案:
【答案】3
【解析】
延长HG交FD于N点,过F点作FM⊥EH,由直角三角形斜边中线性质得AF=EF=BF,利用平移、等腰三角形性质、垂直等条件证明角相等从而可得![]() ,根据相似三角形性质求出AF长,再由勾股定理即可求出BE、FD、EH等线段长,有勾股定理逆定理证明
,根据相似三角形性质求出AF长,再由勾股定理即可求出BE、FD、EH等线段长,有勾股定理逆定理证明![]() 是直角三角形,从而由三角形面积求出斜边的高.
是直角三角形,从而由三角形面积求出斜边的高.
解:延长HG交FD于N点,过F点作FM⊥EH,
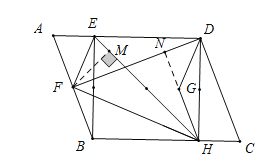
∵![]() 于
于![]() ,即∠BED=∠EBH=90°,
,即∠BED=∠EBH=90°,![]() 为
为![]() 中点,
中点,
∴AF=EF=BF,
∴∠FEB=∠FBE,∠FAE=∠FEA,
由平移性质可知:∠HDE=∠DHB=90°,∠GHD=∠GDH=∠FEB=∠FBE,∠AEF=∠GDA,
∴四边形BHDE是矩形,
∴BH=DE=8,
∵![]() 为
为![]() 的高的交点,
的高的交点,
∴∠GHD+∠FDH=90°,
又∵∠FDH+∠FDA=90°,
∴∠FDA=∠GHD,
∴∠FDA=∠ABE,
∴∠AFD=∠AEB=90°,
又∵∠A=∠A,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
∴在![]() 中,
中,![]()
在![]() 中,
中,![]()
在![]() 中,
中,![]()
易证![]()
∴在![]() 中
中![]() ,
,
∴![]() 是直角三角形,∠EFH=90°,
是直角三角形,∠EFH=90°,
∴![]() ,即
,即![]() ,
,
∴![]() .即
.即![]() 到
到![]() 的距离为3.
的距离为3.
故答案为:3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小欣设计的“利用等腰三角形做菱形”的尺规作图过程.
己知:等腰

求作:点
 ,使得四边形
,使得四边形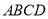 为菱形.
为菱形.做法:①作
 的角平分线
的角平分线 ,交线段
,交线段 于点
于点 ;
;②以点
 为圆心,
为圆心, 长为半径圆弧,交
长为半径圆弧,交 的延长线于点
的延长线于点 ;
;③连接
 ,所以四边形
,所以四边形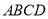 为菱形,点
为菱形,点 即为所求.
即为所求.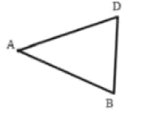
根据小新设计的尺规作图过程.
(1)使用直尺和圆规补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:
 平分
平分 ,
, (______________________________________)(填推理的依据)
(______________________________________)(填推理的依据)
∴四边形
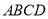 为平行四边形(______________________________________)(填推理的依据)
为平行四边形(______________________________________)(填推理的依据) ,
,∴四边形
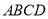 为菱形(______________________________________)(填推理的依据)
为菱形(______________________________________)(填推理的依据)(3)请你设计一种不同于小欣的,利用等腰
 (其中
(其中 )作菱形
)作菱形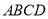 的方法.
的方法.要求:写出简要思路,并尺规作图.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点
 为正方形
为正方形 的边
的边 上任意一点,在正方形内部做等腰直角
上任意一点,在正方形内部做等腰直角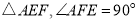 .
.

(1)如图1,若
 ,则
,则 _________(请直接写出答案)
_________(请直接写出答案)(2)作
 关于
关于 的对称点
的对称点 ,连接
,连接 交
交 于点
于点 .
.①补全图形1;
②证明:四边形ECHF为平行四边形.
(3)在(2)的条件下,连接
 ,请直接写出
,请直接写出 和
和 之间的数量关系.
之间的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】新定义:在平面直角坐标系
 中,对于任意点
中,对于任意点 ,和直线
,和直线 ,我们称直线
,我们称直线 为点
为点 的伴随直线,反之称点
的伴随直线,反之称点 为直线
为直线 的伴随点;特别的,直线
的伴随点;特别的,直线 (
( 为常数)的伴随点为
为常数)的伴随点为 .
.

如图1,已知
 三个顶点
三个顶点 的坐标分别为
的坐标分别为 .
.(1)点
 的伴随直线的解析式为__________.(请直接写出答案)
的伴随直线的解析式为__________.(请直接写出答案)(2)若直线
 的伴随点是点
的伴随点是点 ,直线
,直线 的伴随点是点
的伴随点是点 ,点
,点 为
为 轴上的动点,当
轴上的动点,当 的周长最小时,求点
的周长最小时,求点 的坐标.
的坐标.(3)点
 是折线段
是折线段 的动点(包括端点
的动点(包括端点 ),若直线
),若直线 是点
是点 的伴随直线,当直线
的伴随直线,当直线 与
与 有且仅有两个公共点时,请直接写出点
有且仅有两个公共点时,请直接写出点 的横坐标
的横坐标 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】【问题情境】
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
【数学模型】
设该矩形的长为x,周长为y,则y与x的函数表达式为y=2(x+
 )(x>0).
)(x>0).【探索研究】
小彬借鉴以前研究函数的经验,先探索函数y=x+
 的图象性质.
的图象性质.(1)结合问题情境,函数y=x+
 的自变量x的取值范围是x>0,下表是y与x的几组对应值.
的自变量x的取值范围是x>0,下表是y与x的几组对应值.
① 写出m的值;
②画出该函数图象,结合图象,得出当x=________时,y有最小值,y最小=________;
提示:在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.试用配方法求函数y=x+
 (x>0)的最小值,解决问题(2).
(x>0)的最小值,解决问题(2).(2)【解决问题】
直接写出“问题情境”中问题的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点.过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△CAN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3的位置时,(2)中的结论是否仍然成立?若成立,试证明之;若不成立,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+1经过点(2,6),且与直线y=
 x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
(1)求抛物线的解析式;
(2)若P是直线AB上方该抛物线上的一个动点,过点P作PD⊥x轴于点D,交AB于点E,求线段PE的最大值;
(3)在(2)的条件,设PC与AB相交于点Q,当线段PC与BE相互平分时,请求出点Q的坐标.
相关试题

