【题目】点![]() 为正方形
为正方形![]() 的边
的边![]() 上任意一点,在正方形内部做等腰直角
上任意一点,在正方形内部做等腰直角![]() .
.


(1)如图1,若![]() ,则
,则![]() _________(请直接写出答案)
_________(请直接写出答案)
(2)作![]() 关于
关于![]() 的对称点
的对称点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
①补全图形1;
②证明:四边形ECHF为平行四边形.
(3)在(2)的条件下,连接![]() ,请直接写出
,请直接写出![]() 和
和![]() 之间的数量关系.
之间的数量关系.
参考答案:
【答案】(1)![]() ;(2)①见解析;②见解析;(3)
;(2)①见解析;②见解析;(3)![]()
【解析】
(1)在![]() 中,利用勾股定理求得
中,利用勾股定理求得![]() ,再在是等腰直角三角形AEF中利用勾股定理即可求解;
,再在是等腰直角三角形AEF中利用勾股定理即可求解;
(2)①按照要求补全图形即可;
②作MN⊥AB,交DC于N,交AB于M,证得△AMF≌△FNE,根据全等三角形的性质证明点F在正方形ABCD的线BD上,设法证明FH=EC,FH∥EC,从而证明结论;
(3)根据②的过程,利用勾股定理证得 ![]() ,
,![]() ,从而得到
,从而得到![]() .
.
(1)∵四边形ABCD是正方形,AB=6,EC=2,
∴AB=AD=DC=6,∠ADE=90![]() ,
,
在![]() 中,AD= 6,DE=DC-EC=6-2=4,
中,AD= 6,DE=DC-EC=6-2=4,
∴![]() ,
,
∵![]() AEF是等腰直角三角形,且∠AFE=90
AEF是等腰直角三角形,且∠AFE=90![]() ,
,
∴AF=EF,
∵![]() ,即
,即![]() ,
,
∴![]() ;
;
(2)①补全图形如图所示:

②如图,过点F作MN⊥AB,交DC于N,交AB于M,连接BD,

∵AB∥CD,MN⊥AB,∠AFE=90![]() ,
,
∴MN⊥CD,
∴∠AFM+∠EFN=90°,∠AFM +∠FAM=90°,
∴∠EFN =∠FAM,
在△AMF和△FNE中,
 ,
,
∴△AMF≌△FNE(AAS),
∴AM=FN,MF=EN,
∵四边形ABCD是正方形,且MN⊥AB,
∴∠BAD=∠ADC=∠AMN=90°,
∴四边形ADNM是矩形,
∴AM=DN,
∴FN=DN,
又MN⊥CD,
∴∠FDN=45°,
∴点F在正方形ABCD的线BD上,
又F、H关于BC对称,
∴MF=FP=PH=EN,FP⊥BC,
∴四边形BPFM是正方形,四边形PCNF是矩形,
∴FP=NC,PC=FN,
∴FH=EC,
∵F、H关于BC对称,
∴FH⊥BC,
∵DC⊥BC,
∴FH∥EC,
∴四边形ECHF为平行四边形;
(3)由②得MF=FP,
∴![]() ,
,
∵AM=DN=FN,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
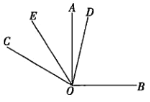
查看答案和解析>>【题目】如图,在同一个平面内,
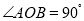 ,
,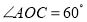 .
.
(1)填空:
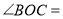 ________;
________;(2)如果OD平分
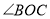 ,OE平分
,OE平分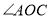 ,那么
,那么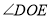 的度数为;
的度数为;(3)试问在(2)的条件下,如果将题目中
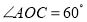 改为
改为 ,其他条件不变,你能求出
,其他条件不变,你能求出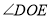 的度数吗?若能,请你写出求解过程;若不能,请说明理由.
的度数吗?若能,请你写出求解过程;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 为
为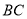 边上一点,连接
边上一点,连接 ,以
,以 为邻边作
为邻边作 与
与 相交于点
相交于点 ,且满足
,且满足 .
.
(1)求证:四边形
 为矩形;
为矩形;(2)若
 ,连接
,连接 ,求
,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小欣设计的“利用等腰三角形做菱形”的尺规作图过程.
己知:等腰

求作:点
 ,使得四边形
,使得四边形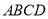 为菱形.
为菱形.做法:①作
 的角平分线
的角平分线 ,交线段
,交线段 于点
于点 ;
;②以点
 为圆心,
为圆心, 长为半径圆弧,交
长为半径圆弧,交 的延长线于点
的延长线于点 ;
;③连接
 ,所以四边形
,所以四边形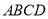 为菱形,点
为菱形,点 即为所求.
即为所求.
根据小新设计的尺规作图过程.
(1)使用直尺和圆规补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:
 平分
平分 ,
, (______________________________________)(填推理的依据)
(______________________________________)(填推理的依据)
∴四边形
 为平行四边形(______________________________________)(填推理的依据)
为平行四边形(______________________________________)(填推理的依据) ,
,∴四边形
 为菱形(______________________________________)(填推理的依据)
为菱形(______________________________________)(填推理的依据)(3)请你设计一种不同于小欣的,利用等腰
 (其中
(其中 )作菱形
)作菱形 的方法.
的方法.要求:写出简要思路,并尺规作图.

-
科目: 来源: 题型:
查看答案和解析>>【题目】新定义:在平面直角坐标系
 中,对于任意点
中,对于任意点 ,和直线
,和直线 ,我们称直线
,我们称直线 为点
为点 的伴随直线,反之称点
的伴随直线,反之称点 为直线
为直线 的伴随点;特别的,直线
的伴随点;特别的,直线 (
( 为常数)的伴随点为
为常数)的伴随点为 .
.

如图1,已知
 三个顶点
三个顶点 的坐标分别为
的坐标分别为 .
.(1)点
 的伴随直线的解析式为__________.(请直接写出答案)
的伴随直线的解析式为__________.(请直接写出答案)(2)若直线
 的伴随点是点
的伴随点是点 ,直线
,直线 的伴随点是点
的伴随点是点 ,点
,点 为
为 轴上的动点,当
轴上的动点,当 的周长最小时,求点
的周长最小时,求点 的坐标.
的坐标.(3)点
 是折线段
是折线段 的动点(包括端点
的动点(包括端点 ),若直线
),若直线 是点
是点 的伴随直线,当直线
的伴随直线,当直线 与
与 有且仅有两个公共点时,请直接写出点
有且仅有两个公共点时,请直接写出点 的横坐标
的横坐标 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
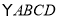 ,
,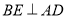 于
于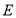 ,
,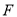 为
为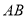 中点,连接
中点,连接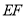 ,将
,将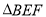 向右平移到
向右平移到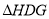 ,使
,使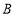 与
与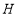 重合,
重合,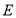 与
与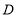 重合,
重合,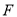 与
与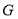 重合,连接
重合,连接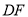 ,
,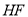 ,
,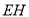 ,若
,若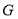 为
为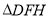 的高的交点,
的高的交点,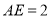 ,
,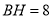 ,则
,则 到
到 的距离为________.
的距离为________.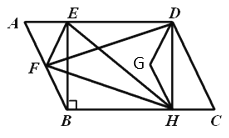
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题情境】
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
【数学模型】
设该矩形的长为x,周长为y,则y与x的函数表达式为y=2(x+
 )(x>0).
)(x>0).【探索研究】
小彬借鉴以前研究函数的经验,先探索函数y=x+
 的图象性质.
的图象性质.(1)结合问题情境,函数y=x+
 的自变量x的取值范围是x>0,下表是y与x的几组对应值.
的自变量x的取值范围是x>0,下表是y与x的几组对应值.
① 写出m的值;
②画出该函数图象,结合图象,得出当x=________时,y有最小值,y最小=________;
提示:在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.试用配方法求函数y=x+
 (x>0)的最小值,解决问题(2).
(x>0)的最小值,解决问题(2).(2)【解决问题】
直接写出“问题情境”中问题的结论.

相关试题

