【题目】如图,![]() 的对角线
的对角线![]() 与
与![]() 相交于点E,点G为
相交于点E,点G为![]() 的中点,连接
的中点,连接![]() ,
,![]() 的延长线交
的延长线交![]() 的延长线于点F,连接
的延长线于点F,连接![]() .
.
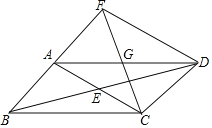
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,判断四边形
,判断四边形![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
参考答案:
【答案】(1)证明见解析;(2)矩形,证明见解析
【解析】
(1)根据ASA定理证得△AGF≌△DGC,从而得到GF=GC,求得四边形ACDF是平行四边形,然后根据平行四边形的性质求证![]()
![]() ;
;
(2)利用平行四边形的判定与性质结合全等三角形的性质得出△AFG是等边三角形,从而得到AD=CF,再利用矩形的判定方法得出答案.
解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠FAG=∠CDG,
∵点G是AD的中点,
∴GA=GD,
在△AGF和△DGC中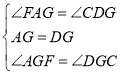 ,
,
∴△AGF≌△DGC(ASA);
∴GF=GC,AF=DC
∴四边形ACDF是平行四边形
∴AC=DF
又∵在平行四边形ABCD中,![]()
∴![]() ;
;
(2)解:四边形ACDF是矩形.
理由:由(1)可知四边形是ACDF平行四边形,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴AB=AF,
又∵AG=AB,
∴AG=AF,
∴AB=AG=AF,
∵四边形ABCD是平行四边形,AD∥BC,∠BCD=120°
∴∠BAD=120°,∠FAG=60°,
∴△AFG是等边三角形,
∴AG=GF,
∵△AGF≌△DGC,
∴FG=CG,
∵AG=GD,
∴AD=CF,
∴四边形ACDF是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,垂足为F,求∠BAC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解分式方程、分式的化简求值
(1)
 ;
;(2)
 ;
;(3)
 ,其中
,其中 ;
;(4)
 ,其中x是不等式组
,其中x是不等式组 的解集中符合题意的整数.
的解集中符合题意的整数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.

(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
 中,点E是对角线
中,点E是对角线 上一点,连接
上一点,连接 .过点E作
.过点E作 交
交 的延长线于点F.若
的延长线于点F.若 ,
, ,则正方形
,则正方形 的面积为______.
的面积为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某区民用电的计费方式为:白天时段的单价为m元/度,晚间时段的单价为n元/度.某户8月份白天时段用电量比晚间时段多50%,9月份白天时段用电量比8月份白天时段用电量少60%,结果9月份的总用电量虽比8月份的总用电量多20%,但9月份的总电费却比8月份的总电费少10%,则
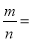 ______.
______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
 中
中 ,E为对角线
,E为对角线 上一点,F是
上一点,F是 延长线上一点,连接
延长线上一点,连接 ,
, ,
, ,
, ,
, .
.
(1)求证:
 ;
;(2)若点G为
 的中点,连接
的中点,连接 ,求证:
,求证: .
.
相关试题

