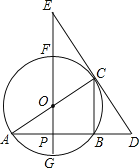
【题目】如图,⊙O中,FG、AC是直径,AB是弦,FG⊥AB,垂足为点P,过点C的直线交AB的延长线于点D,交GF的延长线于点E,已知AB=4,⊙O的半径为![]() .
.
(1)分别求出线段AP、CB的长;
(2)如果OE=5,求证:DE是⊙O的切线;
(3)如果tan∠E=![]() ,求DE的长.
,求DE的长.
参考答案:
【答案】(1)CB=2,AP =2;(2)证明见解析;(3)DE=![]() .
.
【解析】
(1)根据圆周角定理由AC为直径得∠ABC=90°,在Rt△ABC中,根据勾股定理可计算出BC=2,再根据垂径定理由直径FG⊥AB得到AP=BP=![]() AB=2;
AB=2;
(2)易得OP为△ABC的中位线,则OP=![]() BC=1,再计算出
BC=1,再计算出![]() ,根据相似三角形的判定方法得到△EOC∽△AOP,根据相似的性质得到∠OCE=∠OPA=90°,然后根据切线的判定定理得到DE是⊙O的切线;
,根据相似三角形的判定方法得到△EOC∽△AOP,根据相似的性质得到∠OCE=∠OPA=90°,然后根据切线的判定定理得到DE是⊙O的切线;
(3)根据平行线的性质由BC∥EP得到∠DCB=∠E,则tan∠DCB=tan∠E=![]() ,在Rt△BCD中,根据正切的定义计算出BD=3,根据勾股定理计算出CD=
,在Rt△BCD中,根据正切的定义计算出BD=3,根据勾股定理计算出CD=![]() ,然后根据平行线分线段成比例定理得
,然后根据平行线分线段成比例定理得![]() ,再利用比例性质可计算出DE=
,再利用比例性质可计算出DE=![]() .
.
解:(1)∵AC为直径,
∴∠ABC=90°,
在Rt△ABC中,AC=2![]() ,AB=4,
,AB=4,
∴BC=![]() =2,
=2,
∵直径FG⊥AB,
∴AP=BP=![]() AB=2;
AB=2;
(2)∵AP=BP,
∴OP为△ABC的中位线,
∴OP=![]() BC=1,
BC=1,
∴![]() ,
,
而![]() ,
,
∴![]() ,
,
∵∠EOC=∠AOP,
∴△EOC∽△AOP,
∴∠OCE=∠OPA=90°,
∴OC⊥DE,
∴DE是⊙O的切线;
(3)∵BC∥EP,
∴∠DCB=∠E,
∴tan∠DCB=tan∠E=![]()
在Rt△BCD中,BC=2,tan∠DCB=![]() =
=![]() ,
,
∴BD=3,
∴CD=![]() =
=![]() ,
,
∵BC∥EP,
∴![]() ,即
,即![]() ,
,
∴DE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】房山某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.小华与小明同学就“最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下的两个统计图.请根据下面两个不完整的统计图回答以下问题:

(1)这次抽样调查中,共调查了 名学生;
(2)补全两幅统计图;
(3)根据抽样调查的结果,估算该校1000名学生中大约有多少人选择“小组合作学习”?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘轮船以每小时40海里的速度在海面上航行,当该轮船行驶到B处时,发现灯塔C在它的东北方向,轮船继续向北航行,30分钟后到达A处,此时发现灯塔C在它的北偏东75°方向上,求此时轮船与灯塔C的距离.(结果保留根号)

-
科目: 来源: 题型:
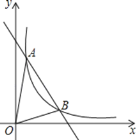
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数
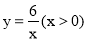 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.(1)求一次函数的解析式;
(2)根据图象直接写出
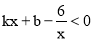 的x的取值范围;
的x的取值范围;(3)求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 在三边互不相等的△ABC中, D,E,F分别是AB,AC,BC边的中点.连接DE,过点C作CM∥AB交DE的延长线于点M,连接CD、EF交于点N,则图中全等三角形共有( )
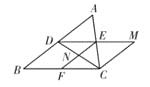
A.3对B.4对C.5对D.6对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,弦AB垂直平分半径OC,垂足为D.若点P是⊙O上异于点A,B的任意一点,则∠APB=( )
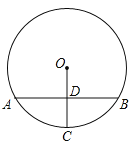
A.30°或60°B.60°或150°C.30°或150°D.60°或120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线M:y=-
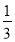 x2+2向左平移2个单位,再向上平移1个单位,得到抛物线M'.若抛物线M'与x轴交于A、B两点,M'的顶点记为C,则∠ACB=( )
x2+2向左平移2个单位,再向上平移1个单位,得到抛物线M'.若抛物线M'与x轴交于A、B两点,M'的顶点记为C,则∠ACB=( )A.45°B.60°C.90°D.120°
相关试题

