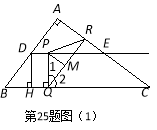
【题目】如图,在Rt△ABC中,∠A=90,AB=6,AC=8,D,E分别是边AB,AC的中点,点P从点D出发沿DE方向运动,过点P作PQ⊥BC于Q,过点Q作QR∥BA交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,QR=y.
(1)求点D到BC的距离DH的长;
(2)求y关于x的函数关系式(不要求写自变量的取值范围);
(3)是否存在点P,使△PQR为等腰三角形?若存在,请求出所有满足要求的x的值;若不存在,请说明理由.

参考答案:
【答案】(1)![]() (2)
(2)![]() (3)存在
(3)存在
【解析】
试题分析:(1)根据△RQC∽△ABC,根据相似三角形的对应边成比例可求解DH;
(2)根据三角形的相似比求出y关于x的函数关系式;
(3)画出图形,根据图形进行讨论:
① 当PQ=PR时,过点P作PM⊥QR于M,则QM=RM.由于∠1+∠2=90°,∠C+∠2=90°,∴∠1=∠C.
∴cos∠1=cosC=![]() =
=![]() ,∴
,∴![]() ,即可求出x的值;
,即可求出x的值;
② 当PQ=RQ时,-![]() x+6=
x+6=![]() ,x=6;
,x=6;
③当PR=QR时,则R为PQ中垂线上的点,于是点R为EC的中点,故CR=![]() CE=
CE=![]() AC=2.
AC=2.
试题解析:(1)![]()
![]() ,AB=6,AC=8,
,AB=6,AC=8,![]() .
.
![]() 点D为AB中点,
点D为AB中点,![]() .
.
![]() ,
,![]() .
.
![]() ,
,![]() ,
,
∴![]() ,
,
(2)![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
即![]() 关于
关于![]() 的函数关系式为:
的函数关系式为:![]() .
.
(3)存在,分三种情况:
①如图(1),当![]() 时,过点P作
时,过点P作![]() 于M,则
于M,则![]() .
.
![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,
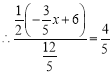 ,
,
![]() .
.
②如图(2),当![]() 时,
时,

![]() ,
,
![]() .
.
③如图(3),当![]() 时,则R为PQ中垂线上的点,于是点R为EC的中点,
时,则R为PQ中垂线上的点,于是点R为EC的中点,
![]() .
.
![]() ,
,
 ,
,
![]() .
.
综上所述,当![]() 为
为![]() 或6或
或6或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.

-
科目: 来源: 题型:
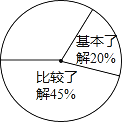
查看答案和解析>>【题目】某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问 卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成 了不完整的表格和扇形统计图(如图).
等级
非常了解
比较了解
基本了解
不太了解
频数
50
m
40
20
根据以上提供的信息解答下列问题:
(1)本次问卷调查共抽取的学生数为 人,表中m的值为 ;
(2)计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数,并补全扇形统计图;
(3)若该校有学生2000人,请根据调查结果估计这些学生中“不太了解”梅山文化知识的人数约为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将二次函数y=x2图象向左平移1个单位,再向下平移2个单位后,所得图象的函数是( )
A.y=(x+1)2+2
B.y=(x﹣1)2﹣2
C.y=(x+1)2﹣2
D.y=(x﹣1)2+2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆锥的底面半径为3,母线为8,则圆锥的侧面积等于_______.
-
科目: 来源: 题型:
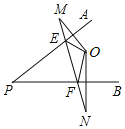
查看答案和解析>>【题目】如图,已知点O是∠APB内的一点,M,N分别是点O关于PA、PB的对称点,连接MN,与PA、PB分别相交于点E、F,已知MN=6cm.
(1)求△OEF的周长;
(2)连接PM、PN,若∠APB=ɑ,求∠MPN(用含ɑ的代数式表示);
(3)当∠ɑ=30°,判定△PMN的形状,并说明理由.
-
科目: 来源: 题型:
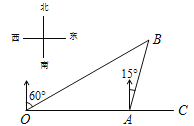
查看答案和解析>>【题目】如图,港口A在观测站O的正东方向,OA=40海里,某船从港口A出发,沿北偏东15°方向航行半小时后到达B处,此时从观测站O处测得该船位于北偏东60°的方向.求该船航行的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工程承包方指定由甲、乙两个工程队完成某项工程,若由甲工程队单独做需要40天完成,现在甲、乙两个工程队共同做20天后,由于甲工程队另有其它任务不再做该工程,剩下工程由乙工程队再单独做了20天才完成任务.
(1)求乙工程队单独完成该工程需要多少天?
(2)如果工程承包方要求乙工程队的工作时间不能超过30天,要完成该工程,甲工程队至少要工作多少天?
相关试题

