搜索
【题目】为了响应“足球进校园”的目标，某校计划为学校足球队购买一批足球，已知购买2个A品牌的足球和3个B品牌的足球共需380元；购买4个A品牌的足球和2个B品牌的足球共需360元．
（1）求A，B两种品牌的足球的单价．
（2）求该校购买20个A品牌的足球和2个B品牌的足球的总费用．
参考答案：
【答案】
（1）解：设A品牌的足球的单价为x元/个，B品牌的足球的单价为y元/个，
根据题意得： 
，
解得： 
．
答：A品牌的足球的单价为40元/个，B品牌的足球的单价为100元/个．
（2）解：20×40+2×100=1000（元）．
答：该校购买20个A品牌的足球和2个B品牌的足球的总费用是1000元．
【解析】（1）由“购买2个A品牌的足球和3个B品牌的足球共需380元”可得2 x + 3 y = 380 ；由“购买4个A品牌的足球和2个B品牌的足球共需360元” 可得4 x + 2 y = 360；（2）总费用包括A足球费用和B品牌费用.
-
科目： 来源： 题型：
查看答案和解析>>【题目】十八届五中全会出台了全面实施一对夫妇可生育两个孩子的政策，这是党中央站在中华民族长远发展的战略高度作出的促进人口长期均衡发展的重大举措．二孩政策出台后，某家庭积极响应政府号召，准备生育两个孩子（生男生女机会均等，且与顺序有关）．
（1）该家庭生育两胎，假设每胎都生育一个小孩，求这两个小孩恰好是1男1女的概率；
（2）该家庭生育两胎，假如第一胎生育一个小孩，其第二胎生育一对双胞胎，请你用画树状图或列表的方法，求这三个小孩中至少有一个女孩的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB＝AC，点D在AC上，过点D作DF⊥BC于点F，且BD＝BC＝AD，则∠CDF的度数为_____．
-
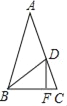
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC角平分线AE、CF交于点P，BD是△ABC的高，点H在AC上，AF＝AH，下列结论：①∠APC＝90°+
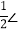ABC；②PH平分∠APC；③若BC＞AB，连接BP，则∠DBP＝∠BAC﹣∠BCA；④若PH∥BD，则△ABC为等腰三角形，其中正确的结论有_____（填序号）．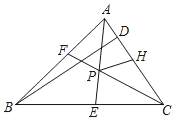
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=ax2+2x﹣3与x轴交于A、B两点，且B（1，0）
（1）求抛物线的解析式和点A的坐标；
（2）如图1，点P是直线y=x上的动点，当直线y=x平分∠APB时，求点P的坐标；
（3）如图2，已知直线y=
x﹣ 
分别与x轴、y轴交于C、F两点，点Q是直线CF下方的抛物线上的一个动点，过点Q作y轴的平行线，交直线CF于点D，点E在线段CD的延长线上，连接QE．问：以QD为腰的等腰△QDE的面积是否存在最大值？若存在，请求出这个最大值；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，D、C、F、B四点在一条直线上，AB=DE，AC⊥BD，EF⊥BD，垂足分别为点C、点F，CD=BF．
求证：（1）△ABC≌△EDF；
（2）AB∥DE．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某工厂现在平均每天比原计划多生产 50 台机器，现在生产 600 台机器所需时间与原计划生产 450 台机器所需时间相同．
（1）现在平均每天生产多少台机器；
（2）生产 3000 台机器，现在比原计划提前几天完成．
相关试题
