Question

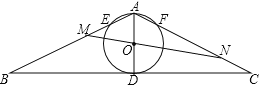
【题目】如图，△ABC中，∠B=∠C=30°，点D是BC边上一点，以AD为直径的⊙O恰与BC边相切，⊙O交A B于E，交AC于F．过O点的直线MN分别交线段BE和CF于M，N，若AM：MB=3：5，则FC：AF的值为（ ）

A.3：1 B.5：3 C.2：1 D.5：2

Answer 1

【答案】A

【解析】

试题分析：根据题意，利用特殊角度建立AN与半径、NC与半径之间的关系，从而求解．根据切线性质，判断出AD⊥BC，根据∠B=∠C=30°，判断出AB=AC，灵活运用等腰三角形的性质和勾股定理解答.

∵∠B=∠C=30°，⊙O恰与BC边相切，AD⊥BC，

∴AB=AC=2AD=2×2r=4r；

连接OE，则OE=OA，

又∵∠BAD=（180°-30°-30°）÷2=60°，

∴OA=AE=OE=r，AB=2AD=4r，

易证△OFN～△MAN，则有OFMA＝FNAN，

又OF=r，MA=3×4r5+3=3r2，FN=AN-r；

解得AN=3r，又AC=AB=4r，则NC=4r- -3r=r；

所以AN：NC=3：1，

故选A．