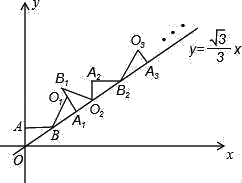
【题目】如图,在平面直角坐标系中,将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线y=![]() x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=
x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=![]() x上,依次进行下去…,若点A的坐标是(0,1),则点A8的横坐标是_____
x上,依次进行下去…,若点A的坐标是(0,1),则点A8的横坐标是_____
参考答案:
【答案】6![]() +6
+6
【解析】
由题知,△AOB为直角三角形,且求出OA=1,AB=![]() ,OB=2;观察可知,△AOB的边都落在直线
,OB=2;观察可知,△AOB的边都落在直线![]() 上,而直线与x轴夹角为30°,则可求出A1的横坐标为(OB+AB)×cos30°;A2的横坐标为(OB+AB+AO)×cos30°,以此类推,找出其中的规律,即可求得A8的横坐标.
上,而直线与x轴夹角为30°,则可求出A1的横坐标为(OB+AB)×cos30°;A2的横坐标为(OB+AB+AO)×cos30°,以此类推,找出其中的规律,即可求得A8的横坐标.
∵点A和点B的纵坐标都为1,
∴AB∥x轴,即AB⊥y轴,
∴△AOB为直角三角形,
OA=1,AB=![]() ,由勾股定理得
,由勾股定理得
![]()
∴OA1=OB+BA1=OB+AB=2+![]() ,
,
由B(![]() ,1)可知,直线
,1)可知,直线![]() 与x轴夹角的正切值为
与x轴夹角的正切值为![]()
则直线![]() 与x轴夹角为30°,
与x轴夹角为30°,
则点A1横坐标的值为OA1×cos30°![]()
点A1纵坐标的值为OA1×sin30°=![]()
∴A1的坐标表示为![]()
以此类推,A2的坐标表示为![]() ,
,
A3的坐标表示为![]()
A4的坐标表示为![]()
根据探索的规律可知,A8的横坐标为![]()
故答案为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
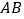 为
为 的直径,
的直径, ,
, 为
为 上的两点,
上的两点, 平分
平分 ,
, 于
于 .
. 求证:
求证: 为
为 的切线;
的切线; 过点
过点 作
作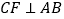 于
于 ,如图
,如图 ,判断
,判断 和
和 ,
, 之间的数量关系,并证明之;
之间的数量关系,并证明之; 若
若 ,
, ,求图中阴影部分的面积.
,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一块长方体木块的各棱长如图所示,一只蜘蛛在木块的一个顶点A处,一只苍蝇在这个长方体上和蜘蛛相对的顶点B处,蜘蛛急于捉住苍蝇,沿着长方体的表面向上爬.

(1)如果D是棱的中点,蜘蛛沿“AD→DB”路线爬行,它从A点爬到B点所走的路程为多少?
(2)若蜘蛛还走前面和右面这两个面,你认为“AD-DB"是最短路线吗?如果不是,请求出最短路程,如果是,请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB、AC于点E、G.连接GF.下列结论:①∠AGD=112.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.
其中正确结论的序号是( )

A. ①②③④⑤ B. ①②③④ C. ①③④⑤ D. ①④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了庆祝新年的到来,我市某中学举行“青春飞扬”元旦汇演,正式表演前,把各班的节目分为A(戏类),B(小品类),C(歌舞类),D(其他)四个类别,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整.请你根据统计图解答下列问题.
(1)参加汇演的节目数共有 个,在扇形统计图中,表示“B类”的扇形的圆心角为 度,图中m的值为 ;
(2)补全条形统计图;
(3)学校决定从本次汇演的D类节目中,选出2个去参加市中学生文艺汇演.已知D类节目中有相声节目2个,魔术节目1个,朗诵节目1个,请求出所选2个节目恰好是一个相声和一个魔术概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为降低空气污染,公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年均载客量如表:
A型
B型
价格(万元/辆)
a
b
年均载客量(万人/年/辆)
60
100
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元
(1)求购买每辆A型公交车和每辆B型公交车分别多少万元?
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车年均载客总和不少于680万人次,有哪几种购车方案?请你设计一个方案,使得购车总费用最少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】周未,小丽骑自行车从家出发到野外郊游,从家出发0.5小时到达甲地,游玩一段时间后按原速前往乙地,小丽离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,行驶10分钟时,恰好经过甲地,如图是她们距乙地的路程y(km)与小丽离家时间x(h)的函数图象.
(1)小丽骑车的速度为 km/h,H点坐标为 ;
(2)求小丽游玩一段时间后前往乙地的过程中y与x的函数关系;
(3)小丽从家出发多少小时后被妈妈追上?此时距家的路程多远.

相关试题

