【题目】甲、乙两工程队维修同一段路面,甲队先清理路面,乙队在甲队清理后铺设路面.乙队在中途停工了一段时间,然后按停工前的工作效率继续工作.在整个工作过程中,甲队清理完的路面长y(米)与时间x(时)的函数图象为线段OA,乙队铺设完的路面长y(米)与时间x(时)的函数图象为折线BC-CD-DE,如图所示,从甲队开始工作时计时.
(1)分别求线段BC、DE所在直线对应的函数关系式.
(2)当甲队清理完路面时,求乙队铺设完的路面长.

参考答案:
【答案】(1)设线段BC所在直线对应的函数关系式为y=k1x+b1,
∵图象经过(3,0)、(5,50),
∴![]() ,解得
,解得![]() 。
。
∴线段BC所在直线对应的函数关系式为y=25x﹣75。
设线段DE所在直线对应的函数关系式为y=k2x+b2.
∵乙队按停工前的工作效率为:50÷(5﹣3)=25,
∴乙队剩下的需要的时间为:(160﹣50)÷25=![]() 。
。
∴点E的横坐标为6.5+![]() =
=![]() 。∴E(
。∴E(![]() ,160)。
,160)。
∴ ,解得
,解得![]() 。
。
∴线段DE所在直线对应的函数关系式为y=25x﹣112.5。
(2)由题意,得
甲队每小时清理路面的长为 100÷5=20,
甲队清理完路面的时间,x=160÷20=8.
把x=8代入y=25x﹣112.5,得y=25×8﹣112.5=87.5。
答:当甲队清理完路面时,乙队铺设完的路面长为87.5米。
【解析】试题分析:(1)求出乙队铺设路面的工作效率,计算出乙队完成需要的时间求出E的坐标,由待定系数法就可以求出结论。
(2)由(1)的结论求出甲队完成的时间,把时间代入乙的解析式就可以求出结论。
-
科目: 来源: 题型:
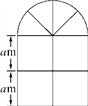
查看答案和解析>>【题目】(12分)如图是某种窗户的形状,其上部是半圆形,下部是边长相同的四个小正方形,已知下部的小正方形的边长为am,计算:
(1)窗户的面积;
(2)窗框的总长;
(3)若a=1,窗户上安装的是玻璃,玻璃每平方米25元,窗框每米20元,窗框的厚度不计,求制作这种窗户需要的费用是多少元(π取3.14,结果保留整数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】大量事实证明,环境污染治理刻不容缓,据统计,全球每分钟约有852.1万吨污水排入江河湖海,把852.1万用科学记数法表示为( )
A. 0.8521×106B. 8521×107C. 8.521×106D. 8.521×107
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:长宽比为
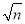 :1(n为正整数)的矩形称为
:1(n为正整数)的矩形称为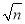 矩形.
矩形.(1)如图1所示,将一张矩形纸片ABCD进行如下操作:将点C沿着过点D的直线折叠,使折叠后的点C落在边AD上的点E处,折痕为DF,通过测量发现DF=AD,则矩形ABCD是
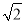 矩形吗?请说明理由.
矩形吗?请说明理由.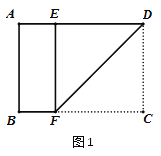
(2)我们可以通过折叠的方式折出一个
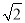 矩形,如图2所示.操作1:将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH.操作2:将AD沿过点G的直线折叠,使点A,点D分别落在边AB,CD上,折痕为EF.所得四边形BCEF为
矩形,如图2所示.操作1:将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH.操作2:将AD沿过点G的直线折叠,使点A,点D分别落在边AB,CD上,折痕为EF.所得四边形BCEF为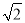 矩形,请说明理由.
矩形,请说明理由.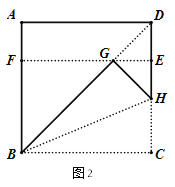
-
科目: 来源: 题型:
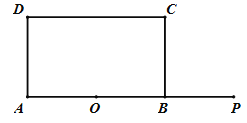
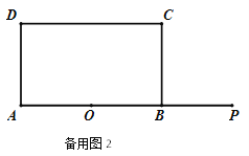
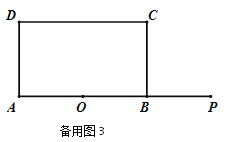
查看答案和解析>>【题目】如图,矩形ABCD中,AB=12,BC=
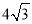 ,点O是AB的中点,点P在AB的延长线上,且BP=6.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动.在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧,设运动的时间为t秒(
,点O是AB的中点,点P在AB的延长线上,且BP=6.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动.在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧,设运动的时间为t秒(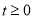 ).
).(1)当t= 时,等边△EFG的边FG恰好经过点C时;
(2)在整个运动过程中,设等边△EFG和矩形ABCD重叠部分的面积为S,请直接写出S与t之间的函数关系式和相应的自变量t的取值范围;
(3)设EG与矩形ABCD的对角线AC的交点为H,是否存在这样的t,使△AOH是等腰三角形?若存在,求出对应的t的值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣3﹣|﹣2| .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程3x2﹣2x﹣4=0的二次项系数、一次项系数、常数项分别为( )
A.3,﹣2,﹣4B.3,2,﹣4C.3,﹣4,2D.2,﹣2,0
相关试题

