【题目】如图,将含60°角的直角三角板ABC绕顶点A顺时针旋转45°度后得到△AB′C′,点B经过的路径为弧BB′,若∠BAC=60°,AC=1,则图中阴影部分的面积是( ) 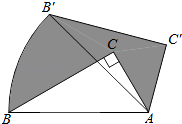
A.![]()
B.![]()
C.![]()
D.π
参考答案:
【答案】A
【解析】解:如图,∵在Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=1, ∴BC=ACtan60°=1× ![]() =
= ![]() ,AB=2
,AB=2
∴S△ABC= ![]() ACBC=
ACBC= ![]() .
.
根据旋转的性质知△ABC≌△AB′C′,则S△ABC=S△AB′C′ , AB=AB′.
∴S阴影=S扇形ABB′+S△AB′C′﹣S△ABC
= ![]()
= ![]() .
.
故选:A.
【考点精析】根据题目的已知条件,利用扇形面积计算公式和旋转的性质的相关知识可以得到问题的答案,需要掌握在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2);①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=50°,则∠EPF=( )度.
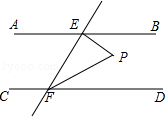
A.70
B.65
C.60
D.55 -
科目: 来源: 题型:
查看答案和解析>>【题目】陈老师和学生做一个猜数游戏,他让学生按照如下步骤进行计算:
①任想一个两位数a,把a乘以2,再加上9,把所得的和再乘以2;
②把a乘以2,再加上30,把所得的和除以2;
③把①所得的结果减去②所得的结果,这个差即为最后的结果.
陈老师说:只要你告诉我最后的结果,我就能猜出你最初想的两位数a.
学生周晓晓计算的结果是96,陈老师立即猜出周晓晓最初想的两位数是31.
请完成
(1)由①可列代数式 ,由②可列代数式 ,由③可知最后结果为 ;(用含a的式子表示)
(2)学生小明计算的结果是120,你能猜出他最初想的两位数是多少吗?
(3)请用自己的语言解释陈老师猜数的方法.
-
科目: 来源: 题型:
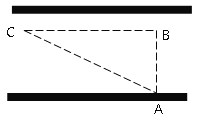
查看答案和解析>>【题目】“道路交通管理条例”规定:小汽车在城街上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A正前方30米B处,过了2秒后,测得小汽车C与车速检测仪A间距离为50米,这辆小汽车超速了吗?
-
科目: 来源: 题型:
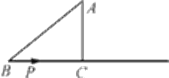
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为ts.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A城气象台测得台风中心在A城正西方向320 km的B处,以每小时40 km的速度向北偏东60°的BF方向移动,距离台风中心200 km的范围内是受台风影响的区域.
(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风影响,那么A城遭受这次台风影响有多长时间?
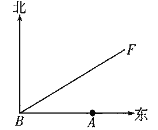
-
科目: 来源: 题型:
查看答案和解析>>【题目】某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
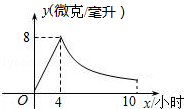
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.
(2)问血液中药物浓度不低于4微克/毫升的持续时间多少小时?
相关试题

