【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫格点,网格中有以格点A、B、C为顶点的△ABC,请你根据所学的知识回答下列问题:

(1)求△ABC的面积;(2)判断△ABC的形状,并说明理由.
参考答案:
【答案】(1)△ABC 的面积为5;(2)△ABC是直角三角形,见解析.
【解析】
(1)三角形ABC面积由长方形面积减去三个直角三角形面积,求出即可;
(2)利用勾股定理表示出AB2=5,BC2=25,AC2=20,再利用勾股定理的逆定理得到三角形为直角三角形.
(1 )S△ABC =4 ×4-![]() ×1×2 -
×1×2 -![]() ×4 ×3-
×4 ×3- ![]() ×2×4 =16-1-6-4=5;
×2×4 =16-1-6-4=5;
(2)△ABC是直角三角形,理由:
∵正方形小方格边长为1
∴AB2=12+22=5,AC2=22+42=20,BC2=32+42=25,
∴AB2+ AC2= BC2,
∴△ABC是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的切线,B为切点,圆心在AC上,∠A=30°,D为
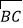 的中点.
的中点.(1)求证:AB=BC;
(2)求证:四边形BOCD是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】x=﹣2是下列( )方程的解.
A.5x+7=7﹣2xB.6x﹣8=8x﹣4C.3x﹣2=4+xD.
 x+2=6
x+2=6 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列条件中,不能判定一个四边形是平行四边形的是( )
A. 两组对边分别平行B. 一组对边平行且相等C. 两组对角分别相等 D. 一组对边相等且一组对角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市提倡“诵读中华经典,营造书香校园”的良好诵读氛围,促进校园文化建设,进而培养学生的良好诵读习惯,使经典之风浸漫校园.某中学为了了解学生每周在校经典诵读时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时)
频数(人数)
频率
2≤t<3
4
0.1
3≤t<4
10
0.25
4≤t<5
a
0.15
5≤t<6
8
b
6≤t<7
12
0.3
合计
40
1
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
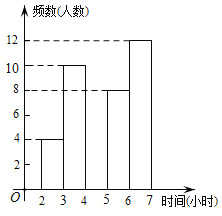
(3)若该校共有1200名学生,试估计全校每周在校参加经典诵读时间至少有4小时的学生约为多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB=6cm,BC=10cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE、DF.
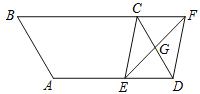
(1)求证:四边形CEDF是平行四边形;(2)当AE的长是多少时,四边形CEDF是矩形?
-
科目: 来源: 题型:
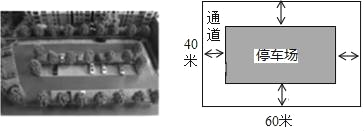
查看答案和解析>>【题目】如图,城市规划部门计划在城市广场的一块长方形空地上修建乙面积为1500m2的停车场,将停车场四周余下的空地修建成同样宽的通道,已知长方形空地的长为60m,宽为40m.
(1)求通道的宽度;
(2)某公司承揽了修建停车场的工程(不考虑修通道),为了尽量减少施工对城市交通的影响,实施施工时,每天的工作效率比原计划增加了20%,结果提前2天完成任务,求该公司原计划每天修建多少m2?
相关试题

