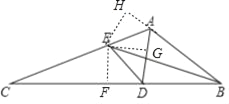
【题目】如图,在△ABC中,∠BAC=120°,AD,BE分别为△ABC的角平分线,连结DE.
(1)求证:点E到DA,DC的距离相等;
(2)求∠DEB的度数.

参考答案:
【答案】(1)见解析;(2)30°.
【解析】
(1)过E作EH⊥AB于H,EF⊥BC于F,EG⊥AD于G,
∵AD平分∠BAC,∠BAC=120°,
∴∠BAD=∠CAD=60°,
∵∠CAH=180°﹣120°=60°,
∴AE平分∠HAD,
∴EH=EG,
∵BE平分∠ABC,EH⊥AB,EF⊥BC,
∴EH=EF,
∴EF=EG,
∴点E到DA、DC的距离相等;
(2)解:∵由(1)知:DE平分∠ADC,
∴∠EDC=∠DEB+∠DBE,
∴![]() =∠DEB+
=∠DEB+![]() ∠ABC,
∠ABC,
∴∠DEB=![]() (∠CDA﹣∠ABC)=
(∠CDA﹣∠ABC)=![]() ∠BAD=30°.
∠BAD=30°.
-
科目: 来源: 题型:
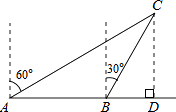
查看答案和解析>>【题目】如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于海里.
-
科目: 来源: 题型:
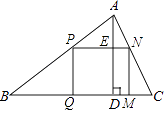
查看答案和解析>>【题目】如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成长方形零件PQMN,使长方形PQMN的边QM在BC上,其余两个顶点P,N分别在AB,AC上,求这个长方形零件PQMN面积S的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有一个轴对称图形,A(3,-2),B(3,﹣6)两点在此图形上且互为对称点,若此图形上有一个点C(﹣2,+1).
(1)求点C的对称点的坐标.
(2)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.
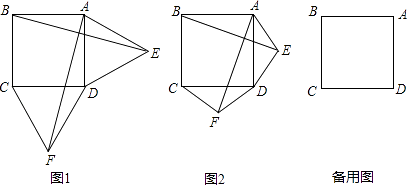
(1)请判断:AF与BE的数量关系是 , 位置关系是;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予说明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断. -
科目: 来源: 题型:
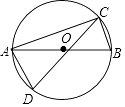
查看答案和解析>>【题目】如图,C,D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=30°,则∠CAB=( )
A.15°
B.20°
C.25°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】下列3×3网格图都是由9个相同的小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:
(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形;
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形;
(3)选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形.
(请将三个小题依次作答在图1、图2、图3中,均只需画出符合条件的一种情形)

相关试题

