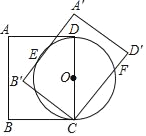
【题目】如图,在矩形ABCD中,AB=6,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A'B'CD'的边A'B'与⊙O相切,切点为E,边CD'与⊙O相交于点F,则CF的长为_____.
参考答案:
【答案】4![]()
![]()
【解析】
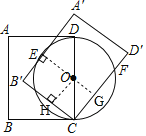
连接OE,延长EO交CD于点G,作OH⊥B′C,由旋转性质知∠B′=∠B′CD′=90°、AB=CD=6,BC=B′C=4,从而得出四边形OEB′H和四边形EB′CG都是矩形且OE=OD=OC=3,继而求得CG=B′E=OH=![]() ,根据垂径定理可得CF的长.
,根据垂径定理可得CF的长.
连接OE,延长EO交CD于点G,作OH⊥B′C于点H,
则∠OEB′=∠OHB′=90°,
∵矩形ABCD绕点C旋转所得矩形为A′B′C′D′,
∴∠B′=∠B′CD′=90°,AB=CD=6,BC=B′C=4,
∴四边形OEB′H和四边形EB′CG都是矩形,OE=OD=OC=3,
∴B′H=OE=3,
∴CH=B′C-B′H=1,
∴CG=B′E=OH=![]() ,
,
∵四边形EB′CG是矩形,
∴∠OGC=90°,即OG⊥CD′,
∴CF=2CG=4![]() ,
,
故答案为:4![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 抛物线
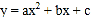 与
与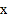 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与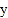 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①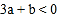 ;②
;②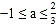 ;③对于任意实数m,
;③对于任意实数m,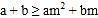 总成立;④关于
总成立;④关于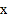 的方程
的方程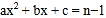 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为

A. 1 个 B. 2 个 C. 3 个 D. 4 个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1,BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论:①△A1AD1≌△CC1B②当x=1时,四边形ABC1D1是菱形 ③当x=2时,△BDD1为等边三角形 ④s=
 (x﹣2)2(0<x<2),其中正确的有( )
(x﹣2)2(0<x<2),其中正确的有( )
A. 1 个B. 2 个C. 3 个D. 4 个
-
科目: 来源: 题型:
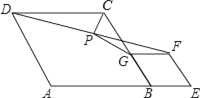
查看答案和解析>>【题目】如图,在菱形ABCD和菱形BEFG中,点A、B、E在同一直线上,P是线段DF的中点,连接PG,PC.若∠ABC=∠BEF=60°,则
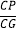 =_____.
=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,BC边上有一点E,BE=4,将纸片折叠,使A点与E点重合,折痕MN交AD于M点,则线段AM的长是_____.
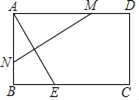
-
科目: 来源: 题型:
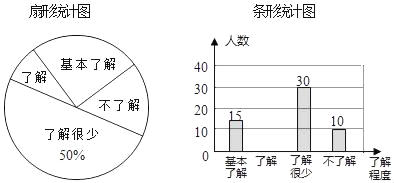
查看答案和解析>>【题目】“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 人,扇形统计图中“了解”部分所对应扇形的圆心角为 °;
(2)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为 人;
(3)若从对校园安全知识达到“了解”程度的3个女生A、B、C和2个男生M、N中分别随机抽取1人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到女生A的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,反比例函数y=
 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
相关试题

