【题目】“中国梦”关乎每个人的幸福生活,为进一步感知我们身边的幸福,展现成都人追梦的风采,我市某校开展了以“梦想中国,逐梦成都”为主题的摄影大赛,要求参赛学生每人交一件作品.现将参赛的50件作品的成绩(单位:分)进行统计如下:
等级 | 成绩(用s表示) | 频数 | 频率 |
A | 90≤s≤100 | x | 0.08 |
B | 80≤s<90 | 35 | y |
C | s<80 | 11 | 0.22 |
合 计 | 50 | 1 |
请根据上表提供的信息,解答下列问题:
(1)表中的x的值为 , y的值为
(2)将本次参赛作品获得A等级的学生依次用A1 , A2 , A3 , …表示,现该校决定从本次参赛作品中获得A等级学生中,随机抽取两名学生谈谈他们的参赛体会,请用树状图或列表法求恰好抽到学生A1和A2的概率.
参考答案:
【答案】
(1)4;0.7
(2)解:依题得获得A等级的学生有4人,用A1,A2,A3,A4表示,画树状图如下:
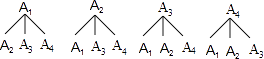
由上图可知共有12种结果,且每一种结果可能性都相同,其中抽到学生A1和A2的有两种结果,
所以从本次参赛作品中获得A等级学生中,随机抽取两名学生谈谈他们的参赛体会,恰好抽到学生A1和A2的概率为:P= ![]()
【解析】解:(1)∵x+35+11=50,∴x=4,或x=50×0.08=4; y= ![]() =0.7,或y=1﹣0.08﹣0.22=0.7;
=0.7,或y=1﹣0.08﹣0.22=0.7;
【考点精析】本题主要考查了列表法与树状图法的相关知识点,需要掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径r=25,四边形ABCD内接于圆⊙O,AC⊥BD于点H,P为CA延长线上的一点,且∠PDA=∠ABD.
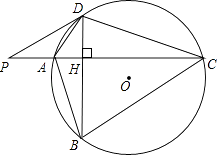
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若tan∠ADB= ,PA=
,PA=  AH,求BD的长;
AH,求BD的长;
(3)在(2)的条件下,求四边形ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知抛物线y=
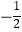 x2+bx+c(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
x2+bx+c(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.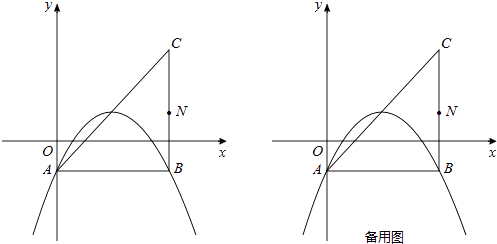
(1)如图,若该抛物线过A,B两点,求该抛物线的函数表达式;
(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q.
(i)若点M在直线AC下方,且为平移前(1)中的抛物线上的点,当以M、P、Q三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点M的坐标;
(ii)取BC的中点N,连接NP,BQ.试探究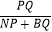 是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出该最大值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算: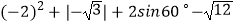
(2)解方程组: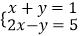 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=x+1的图象与反比例函数
 (k为常数,且k≠0)的图象都经过点A(m,2)
(k为常数,且k≠0)的图象都经过点A(m,2) 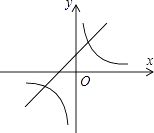
(1)求点A的坐标及反比例函数的表达式;
(2)结合图象直接比较:当x>0时,y1和y2的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,∠B=90°,AB=8cm,BC=6cm,点P从点A开始沿△ABC的边做逆时针运动,且速度为每秒1cm;点Q从点B开始沿△ABC的边做逆时针运动,且速度为每秒2cm,他们同时出发,设运动时间为t秒.
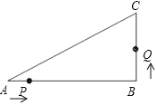
(1)出发2秒后,P,Q两点间的距离为多少cm?
(2)在运动过程中,△PQB能形成等腰三角形吗?若能,请求出几秒后第一次形成等腰三角形;若不能,则说明理由.
(3)出发几秒后,线段PQ第一次把△ABC的周长分成相等两部分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B在线段AC上,点D、E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC.
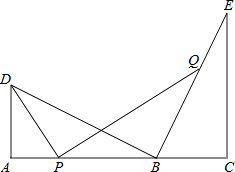
(1)求证:AC=AD+CE;
(2)若AD=3,CE=5,点P为线段AB上的动点,连接DP,作PQ⊥DP,交直线BE于点Q; (i)当点P与A、B两点不重合时,求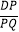 的值;
的值;
(ii)当点P从A点运动到AC的中点时,求线段DQ的中点所经过的路径(线段)长.(直接写出结果,不必写出解答过程)
相关试题

