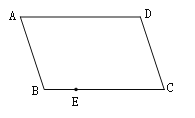
【题目】如图,四边形ABCD是平行四边形,E是BC边上一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE.
(1)作出满足题意的点F,简要说明你的作图过程;
(2)依据你的作图,证明:DF=BE.
参考答案:
【答案】(1)作图见解析;(2)证明见解析.
【解析】(1)如图,连接DE,过B作BF∥DE交AD于F,即可得到结果;
(2)根据平行四边形的性质得到AD∥BC,即DF∥BC,即DF∥BE,由平行四边形的判定定理和性质即可得到结论.
解:(1)正确画出点F,具体作法如下:
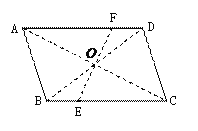
连接AC、BD相交于点O,连接EO并延长EO交AD于点F(或作射线EO交AD于点F.)
(2)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,OD=OB,
∴∠ADO=∠CBO,∠DFO=∠BEO,
∴△DFO≌△BEO,
∴DF=BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
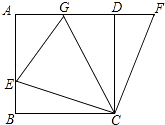
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,OC是∠AOD的平分线,OE是∠BOD的平分线.
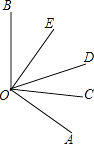
(1)若∠AOB=120°,则∠COE是多少度?
(2)若∠EOC=65°,∠DOC=25°,则∠BOE是多少度? -
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的售价是528元,商家出售一件这样的商品可获利润是进价的10%~20%,设进价为x元,则x的取值范围是 ▲ 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
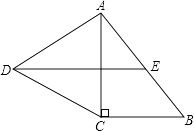
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学团委会开展书法、诵读、演讲、征文四个项目(每人只参加一个项目)的比赛,初三(1)班全体同学都参加了比赛,为了解比赛的具体情况,小明收集整理数据后,绘制了以下不完整的折线统计图和扇形统计图,根据图表中的信息解答下列各题:
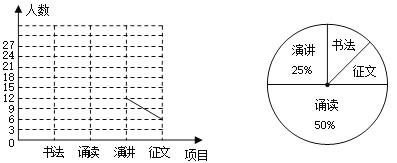
(1)初三(1)班的总人数为 ,扇形统计图中“征文”部分的圆心角度数为 度;
(2)请把折线统计图补充完整;
(3)平平和安安两个同学参加了比赛,请用“列表法”或“画树状图法”,求出他们参加的比赛项目相同的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解,我们把依次连接任意一个四边形各边中点得到的四边形叫中点四边形,如图1,在四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点,依次连接各边中点得到中点四边形EFGH.
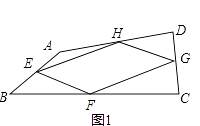
(1)这个中点四边形EFGH的形状是;
(2)如图2,在四边形ABCD中,点M在AB上且△AMD和△MCB为等边三角形,E、F、G、H分别为AB、BC、CD、AD的中点,试判断四边形EFGH的形状并证明.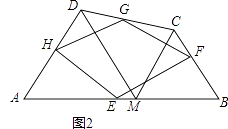
相关试题

