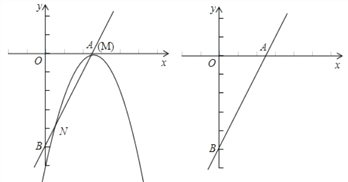
【题目】已知直线y=2x-5与x轴和y轴分别交于点A和点B,抛物线y=-x2+bx+c的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.
(1)如图,当点M与点A重合时,求抛物线的解析式;
(2)在(1)的条件下,求点N的坐标和线段MN的长;
(3)抛物线y=-x2+bx+c在直线AB上平移,是否存在点M,使得△OMN与△AOB相似?若存在,直接写出点M的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)抛物线的解析式![]() ;
;
(2)点N的坐标为![]() ,线段MN的长为
,线段MN的长为![]() ;
;
(3)存在点M(2,-1),或(4,3)
【解析】试题分析:(1)①首先求得直线与x轴,y轴的交点坐标,利用二次函数的对称轴的公式即可求解;
②N在直线上同时在二次函数上,因而设N的横坐标是a,则在两个函数上对应的点的纵坐标相同,据此即可求得a的值,即N的坐标,过N作NC⊥x轴,垂足为C,利用勾股定理即可求得MN的长;
(2)△AOB的三边长可以求得OB=2OA,AB边上的高可以求得是![]() ,抛物线y=-x2+bx+c在直线AB上平移,则MN的长度不变,根据(1)的结果是2
,抛物线y=-x2+bx+c在直线AB上平移,则MN的长度不变,根据(1)的结果是2![]() ,MN是AB边上的高的二倍,当OM⊥AB或ON⊥AB时,两个三角形相似,据此即可求得M的坐标.
,MN是AB边上的高的二倍,当OM⊥AB或ON⊥AB时,两个三角形相似,据此即可求得M的坐标.
试题解析:(1)①∵直线y=2x-5与x轴和y轴交于点A和点B,
∴A(![]() ,0),B(0,-5).
,0),B(0,-5).
当顶点M与点A重合时,
∴M(![]() ,0).
,0).
∴抛物线的解析式是:y=(x![]() )2.即y=x2+5x
)2.即y=x2+5x![]() .
.
②∵N在直线y=2x-5上,设N(a,2a-5),又N在抛物线y=x2+5x![]() 上,
上,
∴2a5=a2+5a![]() .
.
解得a1=![]() ,a2=
,a2=![]() (舍去)
(舍去)
∴N(![]() ,4).
,4).
过N作NC⊥x轴,垂足为C.
∵N(![]() ,4),
,4),
∴C(![]() ,0).
,0).
∴NC=4.MC=OMOC=![]()
![]() =2.
=2.
∴MN=![]() ;
;
(2)设M(m,2m-5),N(n,2n-5).
∵A(![]() ,0),B(0,-5),
,0),B(0,-5),
∴OA=![]() ,OB=5,则OB=2OA,AB=
,OB=5,则OB=2OA,AB=![]() ,
,
当∠MON=90°时,∵AB≠MN,且MN和AB边上的高相等,因此△OMN与△AOB不能全等,
∴△OMN与△AOB不相似,不满足题意.
当∠OMN=90°时, ![]() ,即
,即![]() ,解得OM=
,解得OM=![]() ,
,
则m2+(2m-5)2=(![]() )2,解得m=2,
)2,解得m=2,
∴M(2,-1);

当∠ONM=90°时, ![]() ,即
,即![]() ,解得ON=
,解得ON=![]() ,
,
则n2+(2n-5)2=(![]() )2,解得n=2,
)2,解得n=2,
∵OM2=ON2+MN2,
即m2+(2m-5)2=5+(2![]() )2,
)2,
解得:m=4,
则M的坐标是M(4,3).
故M的坐标是:(2,-1)或(4,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各式
(1)(﹣ )﹣2+(
)﹣2+(  )0+(﹣5)3÷(﹣5)2
)0+(﹣5)3÷(﹣5)2
(2)(x3)2÷x2÷x+x3(﹣x)2(﹣x2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数y=
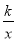 的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )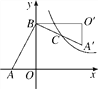
A. 3 B. 4 C. 6 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式m2(a-2)+m(2-a)分解因式,结果正确的是( )
A. m(a-2)(m+1) B. m(a-2)(m-1) C. m(2-a)(m-1) D. m(2-a)(m+1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】选择适当的方法解下列方程:
(1)x2+4x+3=0;
(2) x2﹣x﹣2=0.
x2﹣x﹣2=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】全国体育彩票有一种“22选5”的玩法,中奖的5个号码产生的方法如下:把标有1~22的22个球放进摇奖机中,搅拌均匀后,随机跳出5个球,5个球上的号码就是开奖号码,那么这样产生的中奖号码是简单随机抽样吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明命题“三角形中至少有一个内角大于或等于60°”,第一步应假设 。
相关试题

