【题目】(1)如图1,∠AOB和∠COD都是直角,
①若∠BOC=60°,则∠BOD= °,∠AOC= °;
②改变∠BOC的大小,则∠BOD与∠AOC相等吗?为什么?
(2)如图2,∠AOB=100°,∠COD=110°,若∠AOD=∠BOC+70°,求∠AOC的度数.

参考答案:
【答案】(1)①30;30;②相等,理由详见解析;(2)∠AOC=30°.
【解析】
(1)①根据直角定义可得∠COD=∠AOB=90°,再利用角的和差关系可得答案;
②根据条件可得∠AOB=∠COD,再用等式的性质可得∠AOB-∠COB=∠COD-∠BOC,进而可得结论;
(2)设∠AOC=x°,则∠BOC=(100-x)°,然后再表示出∠BOD,进而可得∠AOD=∠AOB+∠BOD=100°+10°+x°=100°-x°+70°,再解方程即可.
解:(1)①∵∠COD是直角,
∴∠COD=90°,
∵∠BOC=60°,
∴∠BOD=30°,
∵∠AOB是直角,
∴∠AOB=90°,
∵∠BOC=60°,
∴∠AOC=30°,
故答案为:30;30;
②相等,
∵∠AOB和∠COD都是直角,
∴∠AOB=∠COD,
∴∠AOB﹣∠COB=∠COD﹣∠BOC,
即∠BOD=∠AOC;
(2)设∠AOC=x°,则∠BOC=(100﹣x)°,
∵∠COD=110°,
∴∠BOD=110°﹣(100﹣x)°=x°+10°,
∵∠AOD=∠BOC+70°,
∴∠AOD=∠AOB+∠BOD=100°+10°+x°=100°﹣x°+70°,
解得:x=30,
∴∠AOC=30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景
如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形。
类比研究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)。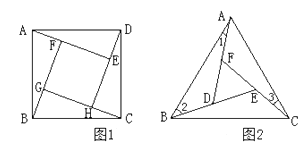
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)进一步探究发现,△ABD的三边存在一定的等量关系,设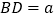 ,
, 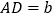 ,
, 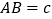 ,请探索
,请探索 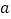 ,
, 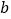 ,
, 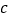 满足的等量关系。
满足的等量关系。 -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC,连结OB,D为OB的中点。点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF。已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒。
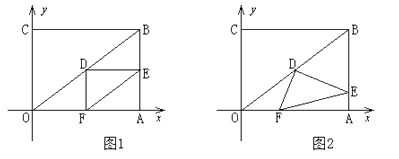
(1)如图1,当t=3时,求DF的长;
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值;
(3)连结AD,当AD将△DEF分成的两部分面积之比为1:2时,求相应t的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,图中的折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象.下列说法错误的是( )
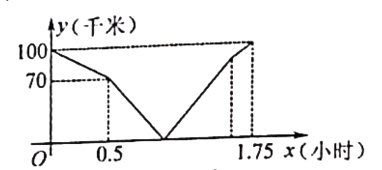
A.乙先出发的时间为0.5小时
B.甲的速度是80千米/小时
C.甲出发0.5小时后两车相遇
D.甲到B地比乙到A地早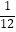 小时
小时 -
科目: 来源: 题型:
查看答案和解析>>【题目】若a>b,则下列各式中一定成立的是( )
A. a﹣3<b﹣3 B.
 C. ﹣3a<﹣3b D. am>bm
C. ﹣3a<﹣3b D. am>bm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知直线 AB、CD 相交于点 O,∠COE=90°
(1)若∠AOC=36°,求∠BOE 的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE 的度数.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923292236627968/1924724835590144/STEM/dc8ee683cff64dfdb92368e07f9f9b9d.png]
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆B位置的坐标;

(2)若体育馆位置坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
相关试题

