【题目】下列计算正确的是( )
A.4a2﹣2a2=2
B.3a+a=3a2
C.4a6÷2a3=2a2
D.﹣2aa=﹣2a2
参考答案:
【答案】D
【解析】解:∵4a2﹣2a2=2a2 ,
∴选项A不正确;
∵3a+a=4a,
∴选项B不正确;
∵4a6÷2a3=2a3 ,
∴选项C不正确;
∵﹣2aa=﹣2a2 ,
∴选项D正确.
故选:D.
【考点精析】掌握单项式乘单项式是解答本题的根本,需要知道单项式与单项式相乘,把他们的系数,相同字母的幂分别相乘,其余字母连同他的指数不变,作为积的因式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市2011年5月1日﹣10日十天的空气污染指数的数据如下(主要污染物为可吸入颗粒物):61,75,70,56,81,91,92,91,75,81.那么该组数据的极差和中位数分别是( )
A. 36,78 B. 36,86 C. 20,78 D. 20,77.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为4cm的等边三角形,动点P从点A出发,以2cm/s的速度沿A→C→B运动,到达B点即停止运动,过点P作PD⊥AB于点D,设运动时间为x(s),△ADP的面积为y(cm2),则能够反映y与x之间函数关系的图象大致是( )
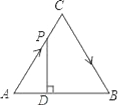
A.
 B.
B.  C.
C. 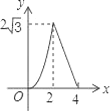 D.
D. 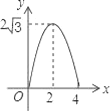
-
科目: 来源: 题型:
查看答案和解析>>【题目】在频数分布直方图中,各小长方形的高等于相应组的( )
A.组距
B.组数
C.频数
D.频率 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,直线EF分别交两直角边AB、BC与E、F两点,且EF∥AC,P是斜边AC的中点,连接PE,PF,且AB=
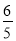 ,BC=
,BC=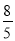 .
.(1)当E、F均为两直角边的中点时,求证:四边形EPFB是矩形,并求出此时EF的长;
(2)设EF的长度为x(x>0),当∠EPF=∠A时,用含x的代数式表示EP的长;
(3)设△PEF的面积为S,则当EF为多少时,S有最大值,并求出该最大值.
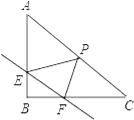
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车车发2h后休息,与甲车相遇后,继续行驶,设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲 , y乙与x之间的函数图象如图所示,结合图象解答下列问题:
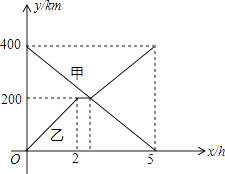
(1)求:y甲与x的函数关系式,并写出自变量x的取值范围;
(2)乙车休息了h;
(3)当两车相距80km时,直接写出x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)【问题情境】
徐老师给爱好学习的小敏和小捷提出这样一个问题:
如图1,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC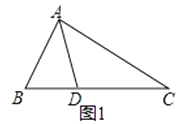
小敏的证明思路是:在AC上截取AE=AB,连接DE.(如图2)…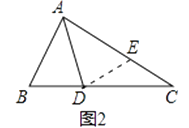
小捷的证明思路是:延长CB至点E,使BE=AB,连接AE. 可以证得:AE=DE(如图3)…
请你任意选择一种思路继续完成下一步的证明.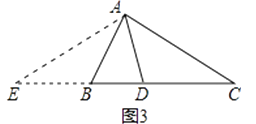
(2)【变式探究】
“AD是∠BAC的平分线”改成“AD是BC边上的高”,其它条件不变.(如图4),AB+BD=AC成立吗?若成立,请证明;若不成立,写出你的正确结论,并说明理由.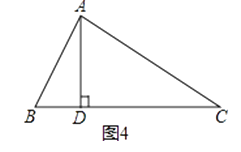
(3)【迁移拓展】
△ABC中,∠B=2∠C. 求证:AC2=AB2+ABBC. (如图5)
相关试题

