【题目】如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD ![]() CD,垂足为D,AD交⊙O 于E,连接CE.
CD,垂足为D,AD交⊙O 于E,连接CE.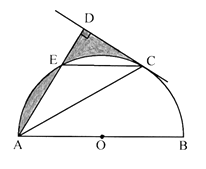
(1)求证:CD 是⊙O 的切线
(2)若E是弧AC的中点,⊙O 的半径为1,求图中阴影部分的面积。
参考答案:
【答案】
(1)证明:∵AC为∠DAB的平分线,∴∠DAC=∠BAC,∵OA=OC,∴∠OAC=∠OCA,∴∠DAC=∠OCA,∴OC∥AD,∵AD⊥CD,∴OC⊥CD,∴CD与圆O相切;
(2)解:连接EB,交OC于F.
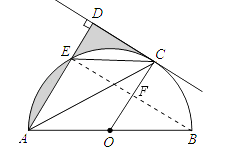
∵E为弧AC的中点,
∴弧AE==弧EC,∴AE=EC,
∴∠EAC=∠ECA.
又∵∠EAC=∠OAC,
∴∠ECA=∠OAC,
∴CE∥OA.
又∵OC∥AD,
∴四边形AOCE是平行四边形,
∴CE=OA,AE=OC.
又∵OA=OC=1,
∴四边形AOCE是菱形.
∵AB为直径,得到∠AEB=90°,
∴EB∥CD.
∵CD与⊙O相切,C为切点,
∴OC⊥CD,
∴OC∥AD,
∵点O为AB的中点,
∴OF为△ABE的中位线,
∴OF= ![]() AE=
AE= ![]() ,即CF=DE=
,即CF=DE= ![]() ,
,
在Rt△OBF中,根据勾股定理得:EF=FB=DC= ![]() ,则S阴影=S△DEC=
,则S阴影=S△DEC= ![]() .
.
【解析】(1)要证CD与圆O相切,需证OC垂直于CD,结合已知条件,由AC为角平分线得到一对角相等,再由OA=OC,利用等边对等角得到一对角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行得到OC与AD平行,根据AD垂直于CD,得到OC垂直于CD,即可得证;
(2)根据E为弧AC的中点,得到弧AE=弧EC,利用等弧对等弦得到AE=EC,可得出弓形AE与弓形EC面积相等,阴影部分面积可转化为为直角三角形DEC的面积,求出S△DEC即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家发改委、工业和信息化部、财政部公布了“节能产品惠民工程”,公交公司积极响应将旧车换成节能环保公交车,计划购买A型和B型两种环保型公交车10辆,其中每台的价格、年载客量如表:
A型
B型
价格(万元/台)
x
y
年载客量/万人次
60
100
若购买A型环保公交车1辆,B型环保公交车2辆,共需400万元;若购买A型环保公交车2辆,B型环保公交车1辆,共需350万元.
(1)求x、y的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保10辆公交车在该线路的年载客量总和不少于680万人次,问有哪几种购买方案?
(3)在(2)的条件下,哪种方案使得购车总费用最少?最少费用是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列条件中,能判定△ABC为直角三角形的是( ).
A.∠A=2∠B-3∠CB.∠A+∠B=2∠CC.∠A-∠B=30°D.∠A=
 ∠B=
∠B= ∠C
∠C -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点E是BC上的一点,EC=2BE,点D是AC的中点.若△ABC的面积S△ABC=12,则S△ADF﹣S△BEF=_____.
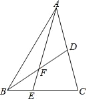
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线
 经过坐标原点,且当
经过坐标原点,且当  时, y随x的增大而减小.
时, y随x的增大而减小.
(1)求抛物线的解析式;
(2)如下图,设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB x轴于点B, DC
x轴于点B, DC  x轴于点C.
x轴于点C.
①当 BC=1时,直接写出矩形ABCD的周长;
②设动点A的坐标为(a, b),将矩形ABCD的周长L表示为a的函数,并写出自变量的取值范围,判断周长是否存在最大值,如果存在,求出这个最大值,并求出此时点A的坐标;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.

下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A.①
B.②
C.①②
D.①③ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B在线段AC上(BC>AB),在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为S3;则S2020﹣S2019=_____.
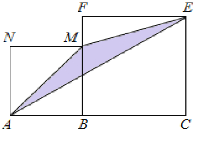
相关试题

