【题目】在平面直角坐标系中,规定把一个三角形先沿着x轴翻折,再向右平移2个单位称为1次变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(﹣1,﹣1)、(﹣3,﹣1),把△ABC经过连续9次这样的变换得到△A′B′C′,则点A的对应点A′的坐标是 . 
参考答案:
【答案】(16,1+ ![]() )
)
【解析】解:∵△ABC是等边三角形,点B、C的坐标分别是(﹣1,﹣1)、(﹣3,﹣1), ∴点A的坐标为(﹣2,﹣1﹣ ![]() ),
),
根据题意得:第1次变换后的点A的对应点的坐标为(﹣2+2,1+ ![]() ),即(0,1+
),即(0,1+ ![]() ),
),
第2次变换后的点A的对应点的坐标为(0+2,﹣1﹣ ![]() ),即(2,﹣1﹣
),即(2,﹣1﹣ ![]() ),
),
第3次变换后的点A的对应点的坐标为(2+2,1+ ![]() ),即(4,1+
),即(4,1+ ![]() ),
),
第n次变换后的点A的对应点的为:当n为奇数时为(2n﹣2,1+ ![]() ),当n为偶数时为(2n﹣2,﹣1﹣
),当n为偶数时为(2n﹣2,﹣1﹣ ![]() ),
),
∴把△ABC经过连续9次这样的变换得到△A′B′C′,则点A的对应点A′的坐标是:(16,1+ ![]() ).
).
故答案为:(16,1+ ![]() ).
).
首先由△ABC是等边三角形,点B、C的坐标分别是(﹣1,﹣1)、(﹣3,﹣1),求得点A的坐标,然后根据题意求得第1次、2次、3次变换后的点A的对应点的坐标,即可得规律:第n次变换后的点A的对应点的为:当n为奇数时为(2n﹣2,1+ ![]() ),当n为偶数时为(2n﹣2,﹣1﹣
),当n为偶数时为(2n﹣2,﹣1﹣ ![]() ),继而求得把△ABC经过连续9次这样的变换得到△A′B′C′,则点A的对应点A′的坐标.
),继而求得把△ABC经过连续9次这样的变换得到△A′B′C′,则点A的对应点A′的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形纸片ABCD中,∠A=60°,将纸片折叠,点A、D分别落在点A′、D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,
 的值为( )
的值为( ) 
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将45°的∠AOB按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数恰为2cm.若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数约为cm.(结果精确到0.1cm,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

-
科目: 来源: 题型:
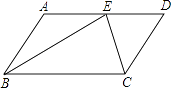
查看答案和解析>>【题目】如图,在ABCD中,AD=10cm,CD=6cm,E为AD上一点,且BE=BC,CE=CD,则DE=cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过点B作BE⊥AC,与BD的垂线DE交于点E.

(1)求证:△ABC≌△BDE;
(2)△BDE可由△ABC旋转得到,利用尺规作出旋转中心O(保留作图痕迹,不写作法). -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学七年级学生共450人,其中男生250人,女生200人.该校对七年级所有学生进行了一次体育测试,并随机抽取了50名男生和40名女生的测试成绩作为样本进行分析,绘制成如下的统计表:
成绩
划记
频数
百分比
不及格

9
10%
及格

18
20%
良好

36
40%
优秀

27
30%
合计
90
90
100%
(1)请解释“随机抽取了50名男生和40名女生”的合理性;
(2)从上表的“频数”,“百分比”两列数据中选择一列,用适当的统计图表示;
(3)估计该校七年级体育测试成绩不及格的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁4名同学进行一次羽毛球单打比赛,要从中选出2名同学打第一场比赛,求下列事件的概率:
(1)已确定甲打第一场,再从其余3名同学中随机选取1名,恰好选中乙同学;
(2)随机选取2名同学,其中有乙同学.
相关试题

