【题目】证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
(1)已知:如图,∠AOC=∠BOC,点P在OC上,
求证: .
请你补全已知和求证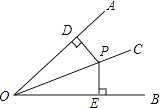
(2)并写出证明过程.
参考答案:
【答案】
(1)PD⊥OA,PE⊥OB;PD=PE
(2)解:已知:PD⊥OA,PE⊥OB,垂足分别为D,E;求证:PD=PE.
∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°,
在△PDO和△PEO中,
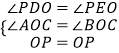 ,
,
∴△PDO≌△PEO(AAS),
∴PD=PE.
故答案为:PD=PE.
【解析】解:∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°,
在△PDO和△PEO中,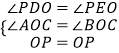 ,
,
∴△PDO≌△PEO(AAS),
∴PD=PE.
根据图形写出已知条件和求证,利用全等三角形的判定得出△PDO≌△PEO,由全等三角形的性质可得结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在坐标平面内有一点P(x,y),若xy=0,那么点P的位置在( )
A. 原点 B. x轴上
C. y轴上 D. 坐标轴上
-
科目: 来源: 题型:
查看答案和解析>>【题目】在比例尺是1:4000的成都市城区地图上,位于锦江区的九眼桥的长度约为3cm,它的实际长度用科学记数法表示为( )
A.12×103cmB.1.2×102mC.1.2×104mD.0.12×105cm
-
科目: 来源: 题型:
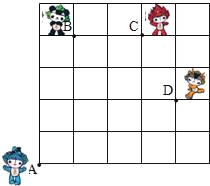
查看答案和解析>>【题目】如图,奥运福娃在5×5的方格(每个格边长尾1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:
B→A(﹣4,﹣1).请根据图中所给信息解决下列问题:
(1)A→C(______),_____);
B→C(______),_____);C→_____(﹣4,﹣3);
(2)如果贝贝的行走路线为A→B→C→D,请计算贝贝走过的路程;
(3)如果贝贝从A处去寻找妮妮的行走路线依次为(+2,+2),
(+2,﹣1),(﹣2,+3),(﹣1,﹣1),请在图中标出妮妮的位置E点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,BE与CD相交于点G,且OE=OD,则AP的长为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:3a3a2﹣2a7÷a2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,BD,CE是高,BD与CE相交于点O

(1)求证:OB=OC;
(2)若∠ABC=50°,求∠BOC的度数.
相关试题

