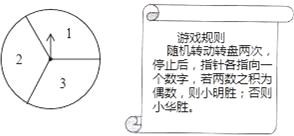
【题目】如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.
(1)现随机转动转盘一次,停止后,指针指向1的概率为 ;
(2)小明和小华利用这个转盘做游戏,若采用下列游戏规则,你认为对双方公平吗?请用列表或画树状图的方法说明理由.
参考答案:
【答案】(1)![]() ;(2)游戏不公平
;(2)游戏不公平
【解析】试题分析:(1)、根据概率的计算法则得出概率;(2)、根据题意进行列表,然后分别得出小明获胜和小华获胜的概率,从而得出答案.
试题解析:(1)、根据题意得:随机转动转盘一次,停止后,指针指向1的概率为![]() ;
;
(2)、列表得:
1 | 2 | 3 | |
1 | (1,1) | (2,1) | (3,1) |
2 | (1,2) | (2,2) | (3,2) |
3 | (1,3) | (2,3) | (3,3) |
所有等可能的情况有9种,其中两数之积为偶数的情况有5种,之积为奇数的情况有4种,
∴P(小明获胜)=![]() ,P(小华获胜)=
,P(小华获胜)=![]() , ∵
, ∵![]() >
>![]() , ∴该游戏不公平.
, ∴该游戏不公平.
-
科目: 来源: 题型:
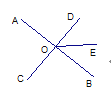
查看答案和解析>>【题目】如图3,直线AB、CD相交于O,若∠AOD比∠AOC大40°,则∠BOD=___°;若∠AOD=2∠AOC,则∠BOC=___;若∠AOD=∠AOC,则∠BOD=___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,直线AB、CD相交于O,OE平分∠BOD,OF平分∠COB,∠2∶∠1=4∶1,求∠AOF的度数.

解:∵OE平分∠BOD
∴∠BOD=__∠1
∵
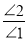 =4
=4 ∴∠2=__∠1
∵∠2+∠BOD=____
∴4∠1+2∠1=
∴∠1=30°
∴∠BOD = ;
∴∠AOC= ;
又∵∠BOD+∠BOC=180°
∴∠BOC=120°
∵ OF平分∠COB
∴∠COF=∠BOF= ;
∴∠AOF=60°+60°= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC沿直线L对折后能与△ADC重合,且AB∥CD,下列选项正确的是( )

A.AB=CD,AO=OC
B.AB=BD,∠BAD=∠DCB
C.AB∥BC,BC=BD
D.OD=OB,∠CDB=∠BCD -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
, 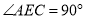 .
.(1)如图①,当
 平分
平分 时,求证:
时,求证: 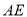 平分
平分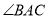 ;
;(2)如图②,移动直角顶点
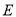 ,使
,使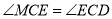 ,求证:
,求证: 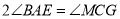 .
.

-
科目: 来源: 题型:
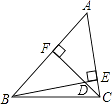
查看答案和解析>>【题目】如图,已知BE和CF是△ABC的两条高,∠ABC=48°,∠ACB=76°,则∠FDE= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=60°,OC平分∠AOB,如果射线OA上的点E满足△OCE是等腰三角形,那么∠OEC的度数为 .

相关试题

