【题目】已知抛物线y=ax2+bx+c(a≠0)与x轴的两个交点的坐标分别是(-3,0),(2,0),则方程ax2+bx+c=0(a≠0)的解是.
参考答案:
【答案】.x1=-3,x2=2
【解析】∵抛物线y=ax2+bx+c(a≠0)与x轴的两个交点的坐标分别是(3,0),(2,0),
∴当x=3或x=2时,y=0,
即方程 ![]() 的解为
的解为 ![]()
所以答案是: ![]()
【考点精析】关于本题考查的抛物线与坐标轴的交点,需要了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】公元前5世纪,毕达哥拉斯学派中的一名成员希伯索斯发现了无理数
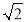 ,导致了第一次数学危机.
,导致了第一次数学危机.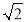 是无理数的证明如下:
是无理数的证明如下:假设
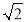 是有理数,那么它可以表示成
是有理数,那么它可以表示成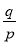 (
(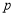 与
与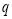 是互质的两个正整数).于是
是互质的两个正整数).于是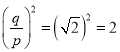 ,所以,
,所以,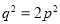 .于是
.于是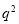 是偶数,进而
是偶数,进而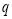 是偶数.从而可设
是偶数.从而可设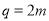 ,所以
,所以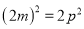 ,
,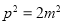 ,于是可得
,于是可得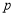 也是偶数.这与“
也是偶数.这与“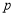 与
与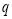 是互质的两个正整数”矛盾,从而可知“
是互质的两个正整数”矛盾,从而可知“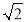 是有理数”的假设不成立,所以,
是有理数”的假设不成立,所以,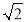 是无理数.这种证明“
是无理数.这种证明“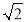 是无理数”的方法是( )
是无理数”的方法是( )A.综合法B.反证法C.举反例法D.数学归纳法
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】某单位为响应政府发出的全民健身的号召,打算在长和宽分别为20 m和11 m的矩形大厅内修建一个60 m2的矩形健身房ABCD.该健身房的四面墙壁中有两侧沿用大厅的旧墙壁(如图为平面示意图),已知装修旧墙壁的费用为20元/m2,新建(含装修)墙壁的费用为80元/m2.设健身房的高为3 m,一面旧墙壁AB的长为x m,修建健身房墙壁的总投入为y元.
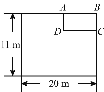
(1)求y与x的函数关系式;
(2)为了合理利用大厅,要求自变量x必须满足条件:8≤x≤12,当投入的资金为4800元时,问利用旧墙壁的总长度为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为2,点A、C在⊙O上,线段BD经过圆心O,∠ABD=∠CDB=90°,AB=1,CD=
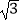 ,则图中阴影部分的面积为 .
,则图中阴影部分的面积为 . 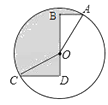
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,DE垂直平分AB,分别交
 的边
的边 、
、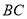 于
于 、
、 ,
, 平分
平分 .设
.设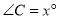 ,
, .
.(1)求
 关于
关于 的函数关系式;
的函数关系式;(2)当
 为等腰三角形时,求∠C的度数.
为等腰三角形时,求∠C的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小丽想用一块面积为
 的正方形纸片,沿着边的方向裁出一块面积为
的正方形纸片,沿着边的方向裁出一块面积为 的长方形纸片,使它的长宽之比为4:3,他不知道能否裁的出来,正在发愁,请你用所学知识帮小丽分析,能否裁出符合要求的纸片.
的长方形纸片,使它的长宽之比为4:3,他不知道能否裁的出来,正在发愁,请你用所学知识帮小丽分析,能否裁出符合要求的纸片.
相关试题

