【题目】如图,在△ABC中,DE垂直平分AB,分别交![]() 的边
的边![]() 、
、![]() 于
于![]() 、
、![]() ,
,![]() 平分
平分![]() .设
.设![]() ,
,![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 为等腰三角形时,求∠C的度数.
为等腰三角形时,求∠C的度数.

参考答案:
【答案】(1)![]() ;(2)∠C=45°或72°.
;(2)∠C=45°或72°.
【解析】
(1)根据线段垂直平分线的性质和角平分线定义求出∠BAC的度数,然后利用三角形内角和定理列式整理可得答案;
(2)分情况讨论:①若∠B=∠BAC,②若∠B=∠C,③若∠C=∠BAC,分别列式计算即可.
解:(1)∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B=![]() ,
,
∵AE平分∠BAC,
∴∠BAC=2∠BAE=![]() ,
,
∵∠B+∠BAC+∠C=180°,
∴![]() ,
,
![]() ;
;
(2)△ABC为等腰三角形时,∠B=∠BAC或∠B=∠C或∠C=∠BAC,
①若∠B=∠BAC,则y=2y,
不符合题意;
②若∠B=∠C,则x=y,
∴![]() ,
,
解得:![]() ;
;
∴![]() ;
;
③若∠C=∠BAC,则![]() ,
,
解得:![]() ,
,
∴![]() ,
,
∴当△ABC为等腰三角形时,∠C=45°或72°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位为响应政府发出的全民健身的号召,打算在长和宽分别为20 m和11 m的矩形大厅内修建一个60 m2的矩形健身房ABCD.该健身房的四面墙壁中有两侧沿用大厅的旧墙壁(如图为平面示意图),已知装修旧墙壁的费用为20元/m2,新建(含装修)墙壁的费用为80元/m2.设健身房的高为3 m,一面旧墙壁AB的长为x m,修建健身房墙壁的总投入为y元.
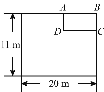
(1)求y与x的函数关系式;
(2)为了合理利用大厅,要求自变量x必须满足条件:8≤x≤12,当投入的资金为4800元时,问利用旧墙壁的总长度为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(a≠0)与x轴的两个交点的坐标分别是(-3,0),(2,0),则方程ax2+bx+c=0(a≠0)的解是.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为2,点A、C在⊙O上,线段BD经过圆心O,∠ABD=∠CDB=90°,AB=1,CD=
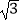 ,则图中阴影部分的面积为 .
,则图中阴影部分的面积为 . 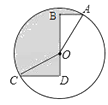
-
科目: 来源: 题型:
查看答案和解析>>【题目】小丽想用一块面积为
 的正方形纸片,沿着边的方向裁出一块面积为
的正方形纸片,沿着边的方向裁出一块面积为 的长方形纸片,使它的长宽之比为4:3,他不知道能否裁的出来,正在发愁,请你用所学知识帮小丽分析,能否裁出符合要求的纸片.
的长方形纸片,使它的长宽之比为4:3,他不知道能否裁的出来,正在发愁,请你用所学知识帮小丽分析,能否裁出符合要求的纸片. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划购买若干台打印机,现从两家商场了解到同一种型号的打印机报价均为1000元,并且多买都有一定的优惠.各商场的优惠条件如下表所示:
商场
优惠条件
甲商场
第一台按原价收费,其余的每台优惠15%
乙商场
每台优惠10%
(1)设公司购买
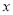 台打印机,选择甲商场时,所需费用为
台打印机,选择甲商场时,所需费用为 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为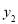 元,请分别求出
元,请分别求出 ,
,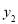 与
与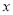 之间的关系式.
之间的关系式.(2)什么情况下,两家商场的收费相同?什么情况下,到甲商场购买更优惠?什么情况下,到乙商场购买更优惠?
(3)现从甲乙两商场一共买入10台打印机,已知甲商场的运费为每台15元,乙商场的运费为每台20元,设总运费为
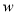 元,从甲商场购买
元,从甲商场购买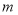 台打印机,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
台打印机,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点
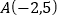 ,
, ,
, ,点
,点 是三角形
是三角形 边
边 上任意一点,三角形经过平移后得到三角形
上任意一点,三角形经过平移后得到三角形 ,点
,点 的对应点为
的对应点为 .
.
(1)直接写出点
 的坐标______________.
的坐标______________.(2)画出三角形
 平移后的三角形
平移后的三角形 .
.(3)在
 轴上是否存在一点
轴上是否存在一点 ,使三角形
,使三角形 的面积等于三角形
的面积等于三角形 面积的
面积的 ,若存在,请求出点
,若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
相关试题

