【题目】△ABC中，∠BAC=90°，AB=AC，点D是BC的中点，把一个三角板的直角顶点放在点D处，将三角板绕点D旋转且使两条直角边分别交AB、AC于E、F .

（1）如图1，观察旋转过程，猜想线段AF与BE的数量关系并证明你的结论；

（2）如图2，若连接EF，试探索线段BE、EF、FC之间的数量关系，直接写出你的结论（不需证明）；

（3）如图3，若将“AB=AC，点D是BC的中点”改为：“∠B=30°，AD⊥BC于点D”，其余条件不变，探索（1）中结论是否成立？若不成立，请探索关于AF、BE的比值.

参考答案：

【答案】（1）证明见解析；（2）；（3）（1）中结论不成立.

【解析】试题分析：（1）连接AD，利用等腰三角形中的三线合一，即可证得AD=BD=DC=BC，∠ADB=∠ADC=90°，又由同角的余角相等，证得∠5=∠4，则可得△BDE≌△ADF，则AF=BE；

（2）由（1）可得AF=BE，AE=CF，又由勾股定理，即可得到；

（3）可证得有两角对应相等，所以可得△BDE∽△ADF，利用三角函数即可求得比值．

（1）如图，连接AD，

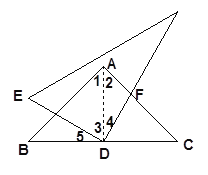
∵AB=AC，∠BAC=90°，点D是BC的中点

∴AD=BD=DC=BC，∠ADB=∠ADC=90°

∴∠B=∠C=∠1=∠2=45°

∴∠3+∠5==90°

∵∠3+∠4==90°

∴∠5=∠4

∵BD=AD

∴△BDE≌△ADF.

∴BE=AF；

（2）根据（1）可得BE=AF，

所以AB-BE=AC-AF，即AE=FC，

∵∠BAC=90°，

∴，

∴

（3）（1）中的结论BE=AF不成立.

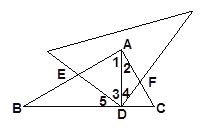
∵∠B=30°，AD⊥BC于点D，∠BAC=90°,

∴∠3+∠5==90°， ∠B+∠1==90°.

∵∠3+∠4==90°，∠1+∠2==90°

∴∠B="∠2" ， ∠5=∠4.

∴△BDE∽△ADF.

∴.

关闭