【题目】实数a、b、c在数轴上的位置如图所示,化简:![]() ﹣|a+c|+
﹣|a+c|+![]() ﹣|﹣2b|.
﹣|﹣2b|.
参考答案:
【答案】解:由数轴可得:c<a<0<b,
则a﹣b<0,a+c<0,c﹣b<0,﹣2b<0,
原式=|a﹣b|﹣|a+c|+|c﹣b|﹣|﹣2b|
=b﹣a+a+c+b﹣c﹣2b
=0
【解析】根据数轴上的点与实数的一一对应关系得到c<a<0<b,则a﹣b<0,a+c<0,c﹣b<0,﹣2b<0,再根据二次根式的性质进行化简,即可解答.
【考点精析】本题主要考查了二次根式的性质与化简的相关知识点,需要掌握1、如果被开方数是分数(包括小数)或分式,先利用商的算数平方根的性质把它写成分式的形式,然后利用分母有理化进行化简.2、如果被开方数是整数或整式,先将他们分解因数或因式,然后把能开得尽方的因数或因式开出来才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=3,BC=4,点P从A点出发,按A→B→C的方向在AB和BC上移动.记PA=x,点D到直线PA的距离为y,则y关于x的函数关系的大致图像是( )
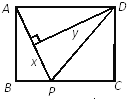
A.
 B.
B. 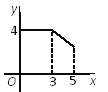 C.
C. 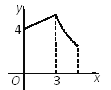 D.
D. 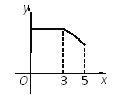
-
科目: 来源: 题型:
查看答案和解析>>【题目】步步高超市某种商品为了去库存,经过两次降价,零售价由100元降为64元.则平均每次降价的百分率是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a﹣2b+1的值是﹣1,则(a﹣2b)2+2a﹣4b的值是( )
A.﹣4
B.﹣1
C.0
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△AOB 中,∠O=90°,AO=8 cm,BO=6 cm,点C 从A 点出发,在边AO 上以2 cm/s 的速度向O 点运动,与此同时,点D 从点B 出发,在边BO 上以1.5 cm/s 的速度向O 点运动,过OC 的中点E 作CD 的垂线EF,则当点C 运动了________s 时,以C点为圆心,2 cm 为半径的圆与直线EF 相切.
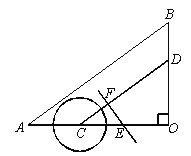
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,解答问题.
例:若代数式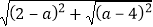 的值是常数2,则a的取值范围 2≤a≤4 .
的值是常数2,则a的取值范围 2≤a≤4 .
分析:原式=|a﹣2|+|a﹣4|,而|a|表示数x在数轴上的点到原点的距离,|a﹣2|表示数a在数轴上的点到数2的点的距离,所以我们可以借助数轴进行分析.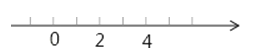
解:原式=|a﹣2|+|a﹣4|
在数轴上看,讨论a在数2表示的点左边;在数2表示的点和数4表示的点之间还是在数4表示的点右边,分析可得a的范围应是2≤a≤4.
(1)此例题的解答过程了用了哪些数学思想?请列举.
(2)化简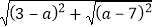 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】2xy(x﹣y)=______.
相关试题

