搜索
【题目】如图，△ABC中，A点坐标为（2，4），B点坐标为（﹣3，﹣2），C点坐标为（3，1）．
（1）在图中画出△ABC关于y轴对称的△A′B′C′（不写画法），并写出点A′，B′，C′的坐标；
（2）求△ABC的面积．
参考答案：
【答案】(1)图略，A’(-2,4) B’(3,-2) C‘（-3，1）;（2）10.5.
【解析】试题分析：（1）根据网格结构找出A′，B′，C′三点的位置，然后顺次连接即可；
（2）利用三角形所在的矩形的面积减去四周三个小三角形的面积，然后列式计算即可.
试题解析：（1）如图所示：
A’(-2,4) B’(3,-2) C‘（-3，1）
（2）S△ABC=6×6-
×5×6-
×6×3-
×1×3=36-15-9-1
=10
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A为函数
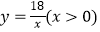图象上一点，连结OA，交函数 
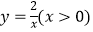的图象于点B，点C是x轴上一点，且AO=AC，求△ABC的面积．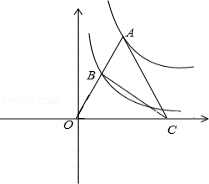 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，书桌上的一种新型台历和一块主板AB、一个架板AC和环扣（不计宽度，记为点A）组成，其侧面示意图为△ABC，测得AC⊥BC，AB=5cm，AC=4cm，现为了书写记事方便，须调整台历的摆放，移动点C至C′，当∠C′=30°时，求移动的距离即CC′的长（或用计算器计算，结果取整数，其中
=1.732， 
=4.583） 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，AP垂直∠ABC的平分线BP于点P．若△ABC的面积为32cm2，BP=6cm,且△APB的面积是△APC的面积的3倍．则AP＝________cm.
-
科目： 来源： 题型：
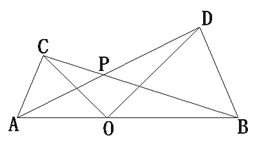
查看答案和解析>>【题目】如图，点O为线段AB上任意一点（不与A、B重合），分别以AO、BO为一腰在AB的同侧作等腰△AOC和等腰△BOD，OA=OC，OB=OD，∠AOC与∠BOD都是锐角，且∠AOC=∠BOD ，AD与BC交于点P.
（1）试说明CB=AD；
（2）若∠COD =80°，求∠APB的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知长方形ABCD，AB=CD， BC=AD，P为长方形ABCD边上的动点，动点P从A出发，沿着A→B→C→D运动到D点停止，速度为2cm/s，设点P用的时间为x秒，△APD的面积为y
，y和x的关系如图2所示.
（1）AB=________cm, BC=______cm;
（2）写出
时,y与x之间的关系式；（3）当y=12时，求x的值；
（4）当P在线段BC上运动时，是否存在点P使得△APD的周长最小，若存在，求出此时∠APD的度数，若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知小红的成绩如下表：
文化成绩
综合素
质成绩
总成绩
测验1
测验2
测验3
小红
560分
580分
630分
12
（1）小红的这三次文化测试成绩的平均分是_____分；
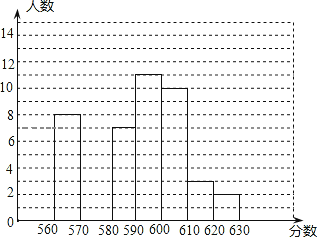
（2）用（1）中的平均分加上综合素质成绩就是小红的总成绩．用同样的方法计算出小红所在班级全部同学的总成绩并绘制出了如图所示的频数分布直方图．那么小红所在班级共有_____名同学；
（3）学校将根据总成绩由高到低保送小红所在班级前15名同学进入高中学习，请问小红能被保送吗？说明理由．
相关试题
