【题目】如图1,已知长方形ABCD,AB=CD, BC=AD,P为长方形ABCD边上的动点,动点P从A出发,沿着A→B→C→D运动到D点停止,速度为2cm/s,设点P用的时间为x秒,△APD的面积为y![]() ,y和x的关系如图2所示.
,y和x的关系如图2所示.

(1)AB=________cm, BC=______cm;
(2)写出![]() 时,y与x之间的关系式;
时,y与x之间的关系式;
(3)当y=12时,求x的值;
(4)当P在线段BC上运动时,是否存在点P使得△APD的周长最小,若存在,求出此时∠APD的度数,若不存在,请说明理由.
参考答案:
【答案】(1)AB=6cm,BC=12cm;(2)y=12x;(3)x=1或11;(4)存在,此时∠APD =90°
【解析】(1)根据函数图象可得从A到B共用了3秒,从B到C用了6秒,速度为2cm/s,则可计算出AB、BC的长度;
(2)由三角形面积公式可得: ,△APD的面积=![]() 和AP=2x可得出y与x之间的关系式;
和AP=2x可得出y与x之间的关系式;
(3)分情况讨论,当点P在AB和CD上时,求得x的值即可;
(4)作A关于直线BC的对称点A′,连接A′D与BC交于点P,根据两边之和大于第三边可知A′D最小,即△APD的周长最小,求出∠APD=∠A′+∠BAP=90°.
(1)∵由函数图象可得:点P从A到B共用了3秒,从B到C用了6秒,点P的速度为2cm/s
∴AB=6cm, BC=12cm;
(2)如图所示:
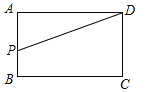
当![]() 时,点P在线段AB上,AP=2x,
时,点P在线段AB上,AP=2x,
∴S△ADP=![]() .
.
(3)如图所示:
分两种情况:
①当P在AB上时,如图所示,当y=3时,3=3x,x=1,

②当P在CD上时,如图所示,则AB+BC+CP=t,
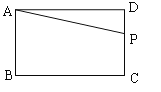
∴PD=3+3+6-t=12-t,
∴y=![]() PDAD=
PDAD=![]() ×6×(12-t)=3(12-t),
×6×(12-t)=3(12-t),
当y=3时,3=3(12-t),
t=11,
综上所述,当y=3时,x的值是1秒或11秒;
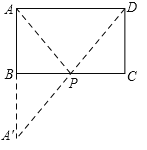
(4)存在,如图所示,延长AB至A′,使AB=A′B,连接A′D,交BC于P,连接AP,
此时△APD的周长最小,
∴AA′=AB+BA′=3+3=6,
∴AD=AA′=6,
∴△A′AD是等腰直角三角形,
∴∠A′=45°,
∵∠ABC=90°,
∴BP是AA′的中垂线,
∴AP=PA′,
∴∠A′=∠BAP=45°,
∴∠APD=∠A′+∠BAP=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AP垂直∠ABC的平分线BP于点P.若△ABC的面积为32cm2,BP=6cm,且△APB的面积是△APC的面积的3倍.则AP=________cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,A点坐标为(2,4),B点坐标为(﹣3,﹣2),C点坐标为(3,1).

(1)在图中画出△ABC关于y轴对称的△A′B′C′(不写画法),并写出点A′,B′,C′的坐标;
(2)求△ABC的面积.
-
科目: 来源: 题型:
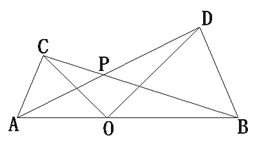
查看答案和解析>>【题目】如图,点O为线段AB上任意一点(不与A、B重合),分别以AO、BO为一腰在AB的同侧作等腰△AOC和等腰△BOD,OA=OC,OB=OD,∠AOC与∠BOD都是锐角,且∠AOC=∠BOD ,AD与BC交于点P.
(1)试说明CB=AD;
(2)若∠COD =80°,求∠APB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知小红的成绩如下表:
文化成绩
综合素
质成绩
总成绩
测验1
测验2
测验3
小红
560分
580分
630分
12
(1)小红的这三次文化测试成绩的平均分是_____分;
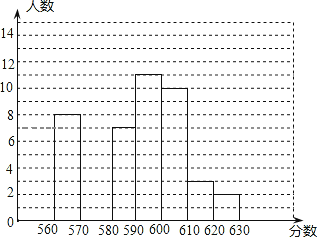
(2)用(1)中的平均分加上综合素质成绩就是小红的总成绩.用同样的方法计算出小红所在班级全部同学的总成绩并绘制出了如图所示的频数分布直方图.那么小红所在班级共有_____名同学;
(3)学校将根据总成绩由高到低保送小红所在班级前15名同学进入高中学习,请问小红能被保送吗?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】麻城市思源实验学校自从开展“高效课堂”模式以来,在课堂上进行当堂检测效果很好.每节课40分钟教学,假设老师用于精讲的时间x(单位:分钟)与学生学习收益量y的关系如图1所示,学生用于当堂检测的时间x(单位:分钟)与学生学习收益y的关系如图2所示(其中OA是抛物线的一部分,A为抛物线的顶点),且用于当堂检测的时间不超过用于精讲的时间.
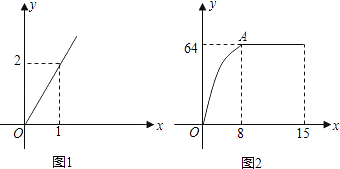
(1)求老师精讲时的学生学习收益量y与用于精讲的时间x之间的函数关系式;
(2)求学生当堂检测的学习收益量y与用于当堂检测的时间x的函数关系式;
(3)问此“高效课堂”模式如何分配精讲和当堂检测的时间,才能使学生在这40分钟的学习收益总量最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
相关试题

