【题目】如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.

参考答案:
【答案】(1)证明见解析;(2)当∠BAC=90°时,矩形AEBD是正方形.理由见解析.
【解析】试题分析:(1)利用平行四边形的判定首先得出四边形AEBD是平行四边形,进而由等腰三角形的性质得出∠ADB=90°,即可得出答案;
(2)利用等腰直角三角形的性质得出AD=BD=CD,进而利用正方形的判定得出即可.
(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,
∴四边形AEBD是平行四边形,
∵AB=AC,AD是∠BAC的角平分线,
∴AD⊥BC,
∴∠ADB=90°,
∴平行四边形AEBD是矩形;
(2)当∠BAC=90°时,
理由:∵∠BAC=90°,AB=AC,AD是∠BAC的角平分线,
∴AD=BD=CD,
∵由(1)得四边形AEBD是矩形,
∴矩形AEBD是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是
 ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )A. 2,
 B. 2,1 C. 4,
B. 2,1 C. 4, D. 4,3
D. 4,3 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个四位数,记千位上和百位上的数字之和为x,十位上和个位上的数字之和为y,如果
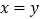 ,那么称这个四位数为“和平数”.例如:
,那么称这个四位数为“和平数”.例如: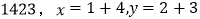 ,因为x=y,所以
,因为x=y,所以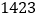 是“和平数”.
是“和平数”.(1)直接写出:最小的“和平数”是________,最大的“和平数”是________;
(2)求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是
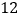 的倍数的所有“和平数”;
的倍数的所有“和平数”;(3)将一个“和平数”的个位上与十位上的数字交换位置,同时,将百位上与千位上的数字交换位置,称交换前后的这两个“和平数”为一组“相关和平数”。例如:
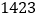 与
与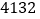 为一组“相关和平数”求证:任意的一组“相关和平数”之和是1111的倍数.
为一组“相关和平数”求证:任意的一组“相关和平数”之和是1111的倍数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在拆线统计图上点的位置__,则数据越大,它反映的是数据波动情况,条形统计图上的__越高,则相应的数据越大,直方图运用长方形的__表示频数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
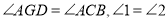 . 求证:CD∥EF.(填空并在后面的括号中填理由)
. 求证:CD∥EF.(填空并在后面的括号中填理由)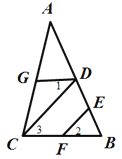
证明:∵∠AGD=∠ACB
∴DG∥___________ (__________)
∴∠3=__________ (_____________)
∵∠1=∠2 (___________________)
∴∠3=__________ (___________________)
∴__________∥___________ (__________________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )

A.0 B.1 C.2 D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,多边形OABCDE的顶点坐标为O(0,0),A(2,0),B(2,2),C(4,2),D(4,4),E(0,4),若如图过点M(1,2)的直线MP(与y轴交于点P)将多边形OABCDE分割成面积相等的两部分,则直线MP的函数表达式是___________.

相关试题

