【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,点G是⊙O上一点,AG交CD于点K,延长KD至点E,使KE=GE,分别延长EG、AB相交于点F.
(1)求证:EF是⊙O的切线;
(2)若AC∥EF,试探究KG、KD、GE之间的关系,并说明理由;
(3)在(2)的条件下,若sinE=![]() ,AK=2
,AK=2![]() ,求FG的长.
,求FG的长.

参考答案:
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)连接OG,首先证明∠EGK=∠EKG,再证明∠HAK+∠KGE=90°,进而得到∠OGA+∠KGE=90°即GO⊥EF,进而证明EF是⊙O的切线;
(2)连接GD,由平行线的性质得到相等的角,进而根据相似三角形的判定得到△GKD∽△EKG,然后根据相似三角形的对应边成比例可得证;
(3)连接OG,OC,根据平行线的性质得到∠E=∠ACH,然后根据已知的sinE=![]() 设出AH=3t,则AC=5t,CH=4t,然后根据勾股定理求出CH、AH的长,设⊙O半径为r,在Rt△OCH中,OC=r,OH=r﹣3
设出AH=3t,则AC=5t,CH=4t,然后根据勾股定理求出CH、AH的长,设⊙O半径为r,在Rt△OCH中,OC=r,OH=r﹣3![]() ,由勾股定理得:OH2+CH2=OC2,求出r的值,再由OG的长和tan∠OFG=tan∠CAH,利用三角函数在Rt△OGF中计算出FG的长.
,由勾股定理得:OH2+CH2=OC2,求出r的值,再由OG的长和tan∠OFG=tan∠CAH,利用三角函数在Rt△OGF中计算出FG的长.
证明:(1)如图1,连接OG.
∵KE=EG,
∴∠EKG=∠EGK,
∵∠AKH=∠EKG,
∴∠EGK=∠AKH,
∴OA=OG,
∴∠OGA=∠OAK,
∵AB⊥CD,
∴∠AHK=90°,
∴∠AKH+∠OAG=90°,
∴∠OGA+∠EGK=90°,
∴∠OGE=90°,
∴EF是⊙O的切线;
(2)KG2=KDGE,理由是:
连接GD,如图2,

∵AC∥EF,
∴∠C=∠E,
∵∠C=∠AGD,
∴∠E=∠AGD,
∵∠GKD=∠GKD,
∴△GKD∽△EKG,
∴![]() ,
,
∴KG2=KDEK,
由(1)得:EK=GE,
∴KG2=KDGE;
(3)连接OG,OC,如图3所示,
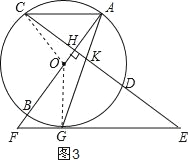
∵AC∥EF,
∴∠E=∠ACH,
∵sinE=sin∠ACH=![]() ,
,
设AH=3t,则AC=5t,CH=4t,
∵KE=GE,AC∥EF,
∴CK=AC=5t,
∴HK=CK﹣CH=t.
在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,
即(3t)2+t2=(2![]() )2,解得t=±
)2,解得t=±![]() .
.
∴CH=4![]() ,AH=3
,AH=3![]() ,
,
设⊙O半径为r,在Rt△OCH中,OC=r,OH=r﹣3![]() ,
,
由勾股定理得:OH2+CH2=OC2,
即(r﹣3![]() )2+(4
)2+(4![]() )2=r2,解得r=
)2=r2,解得r=![]() ,
,
∵EF为切线,
∴△OGF为直角三角形,
在Rt△OGF中,OG=![]() ,tan∠OFG=tan∠CAH=
,tan∠OFG=tan∠CAH=![]() =
=![]() =
=![]() ,
,
∴FG=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(x﹣3)(x﹣4)﹣m2=0.
(1)求证:对任意实数m,方程总有2个不相等的实数根;
(2)若方程的一个根是2,求m的值及方程的另一个根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°.以AB长为一边作△ABD,且AD=BD,∠ADB=90°,取AB中点E,连DE、CE、CD.则∠EDC= °.

-
科目: 来源: 题型:
查看答案和解析>>【题目】重庆市的重大惠民工程﹣﹣公租房建设已陆续竣工,计划10年内解决低收入人群的住房问题,前6年,每年竣工投入使用的公租房面积y(单位:百万平方米),与时间x的关系是y=
 x+5,(x单位:年,1≤x≤6且x为整数);后4年,每年竣工投入使用的公租房面积y(单位:百万平方米),与时间x的关系是y=-
x+5,(x单位:年,1≤x≤6且x为整数);后4年,每年竣工投入使用的公租房面积y(单位:百万平方米),与时间x的关系是y=- x+
x+ (x单位:年,7≤x≤10且x为整数).假设每年的公租房全部出租完.另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金z(单位:元/m2)与时间x(单位:年,1≤x≤10且x为整数)满足一次函数关系如下表:
(x单位:年,7≤x≤10且x为整数).假设每年的公租房全部出租完.另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金z(单位:元/m2)与时间x(单位:年,1≤x≤10且x为整数)满足一次函数关系如下表:z(元/m2)
50
52
54
56
58
…
x(年)
1
2
3
4
5
…
(1)求出z与x的函数关系式;
(2)求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;
(3)若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高a%,这样可解决住房的人数将比第6年减少1.35a%,求a的值.
(参考数据:
 ,
, ,
, )
) -
科目: 来源: 题型:
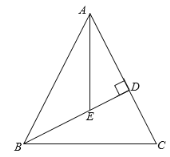
查看答案和解析>>【题目】如图,在等腰△ABC中,AB=AC=10,高BD=8,AE平分∠BAC,则△ABE的面积为________.
-
科目: 来源: 题型:
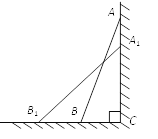
查看答案和解析>>【题目】如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙底端C的距离为0.7米.如果梯子的顶端沿墙面下滑0.4米,那么点B将向左滑动多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.

相关试题

