【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°.以AB长为一边作△ABD,且AD=BD,∠ADB=90°,取AB中点E,连DE、CE、CD.则∠EDC= °.

参考答案:
【答案】75
【解析】
试题分析:根据在直角三角形中,斜边上的中线等于斜边的一半得到EC=EA=EB=![]() AB,根据三角形的外角的性质求出∠CEB=60°,根据直角三角形的性质得到ED=EC,根据三角形内角和定理计算即可.
AB,根据三角形的外角的性质求出∠CEB=60°,根据直角三角形的性质得到ED=EC,根据三角形内角和定理计算即可.
解:∵∠ACB=90°,点E是AB中点,
∴EC=EA=EB=![]() AB,
AB,
∴∠ECA=∠CAB=30°,
∴∠CEB=60°,
∵AD=BD,点E是AB中点,
∴DE⊥AB,即∠AED=90°,
∴∠DEC=180°﹣90°﹣60°=30°,
∵∠ADB=90°,点E是AB中点,
∴DE=![]() AB,
AB,
∴ED=EC,
∴∠EDC=75°,
故答案为:75.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线上,则a的值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东30°、西北(即北偏西45°)方向上又分别发现了客轮B和海岛C.
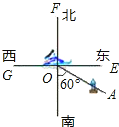
(1)仿照表示灯塔方位的方法,分别画出表示客轮B和海岛C方向的射线OB,OC(不写作法);
(2)若图中有一艘渔船D,且∠AOD的补角是它的余角的3倍,画出表示渔船D方向的射线OD,则渔船D在货轮O的 (写出方位角)
-
科目: 来源: 题型:
查看答案和解析>>【题目】同时抛掷两枚质地均匀的正方体骰子(骰子每一面的点数分别是从1到6这六个数字中的一个),以下说法正确的是( )
A. 掷出两个1点是不可能事件 B. 掷出两个骰子的点数和为6是必然事件
C. 掷出两个6点是随机事件 D. 掷出两个骰子的点数和为14是随机事件
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中:①阴天会下雨;②随机掷一枚均匀的硬币,正面朝上;③12名同学中,有两人的出生月份相同;④2008年奥运会在北京举行.不确定事件有( )个
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列命题:①相等的角是对顶角;②互补的角一定是邻补角;③互补的两个角一定是一个锐角,另一个为钝角;④平行于同一条直线的两直线平行;⑤邻补角的平分线互相垂直.其中,真命题的个数为( )个
A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的三个内角中( )
A. 至少有一个等于90度 B. 至少有一个大于90度
C. 可能只有一个小于90度 D. 不可能都小于60度
相关试题

