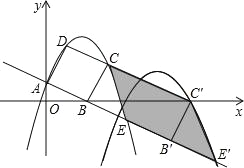
【题目】如图,已知直线![]() 交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.
交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.
(1)求点C、D的坐标
(2)求抛物线的解析式
(3)若抛物线与正方形沿射线AB下滑,直至点C落在x轴上时停止,求抛物线上C、E两点间的抛物线所扫过的面积.
参考答案:
【答案】(1)C(3,2),D(1,3);(2)y=-![]() x2+
x2+![]() x+1;(3)10.
x+1;(3)10.
【解析】
试题分析:(1)分别过C、D两点作x轴、y轴的垂线,利用三角形全等的关系可确定C、D两点的坐标;
(2)根据A、C、D三点的坐标求抛物线解析式;
(3)由平移的性质可判断线段CE所扫过的部分为平行四边形,CC′为底,BC为高,由此求出C、E两点间的抛物线所扫过的面积.
试题解析:(1)如图,分别过C、D两点作x轴、y轴的垂线,垂足为M、N,

由直线AB的解析式得AO=1,OB=2,
由正方形的性质可证△ADN≌△BAO≌△CBM,
∴DN=BM=AO=1,AN=CM=BO=2,
∴C(3,2),D(1,3);
(2)设抛物线解析式为y=ax2+bx+c,
将A(0,1),C(3,2),D(1,3)三点坐标代入,得 ,
,
解得 ,
,
∴y=-![]() x2+
x2+![]() x+1;
x+1;
(3)∵AB=BC=![]() ,
,
由△BCC′∽△AOB,得![]() ,
,
∴CC′=2BC=2![]() ,
,
由割补法可知,抛物线上C、E两点间的抛物线所扫过的面积=SCEE′C′=CC′×BC=2![]() ×
×![]() =10,
=10,
即抛物线上C、E两点间的抛物线所扫过的面积为10.
-
科目: 来源: 题型:
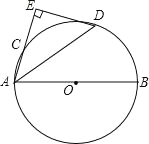
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)如果AD=5,AE=4,求AC长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把抛物线y=2x2先向左平移3个单位,再向上平移4个单位,所得抛物线的函数表达式为( )
A. y=2(x+3)2+4 B. y=2(x+3)2﹣4 C. y=2(x﹣3)2﹣4 D. y=2(x﹣3)2+4
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)某同学在计算多项式M加上x2 -3x+7时,因误认为是加上x2+3x+7,结果得到答案是15x2+2x-4.试问:
(1)M是怎样的整式?
(2)这个问题的正确结果应是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】家用电灭蚊器的发热部分使用了PTC发热材料,它的电阻R(kΩ)随温度t(℃)(在一定范围内)变化的大致图象如图所示.通电后,发热材料的温度在由室温10℃上升到30℃的过程中,电阻与温度成反比例关系,且在温度达到30℃时,电阻下降到最小值;随后电阻随温度升高而增加,温度每上升1℃,电阻增加
 kΩ.
kΩ.(1)求当10≤t≤30时,R和t之间的关系式;
(2)求温度在30℃时电阻R的值;并求出t≥30时,R和t之间的关系式;
(3)家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过6 kΩ?

-
科目: 来源: 题型:
查看答案和解析>>【题目】把下面各式分解因式:(1)ax3-9ax;
(2)x2+2x(x-3y)+(x-3y)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+4x+k=0有两个实数根,则k的取值范围是( )
A. k≤﹣4 B. k<﹣4 C. k≤4 D. k<4
相关试题

