【题目】如图,动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,3s后,两点相距15个单位长度.已知动点A、B的速度比是1:4(速度单位:单位长度/s).
![]()
(1)求出两个动点运动的速度,并在数轴上标出A、B两点从原点出发运动3s时的位置;
(2)若A、B两点从(1)中的位置同时向数轴负方向运动,几秒时,原点恰好处在两个动点的正中间?
(3)在(2)中原点恰好处在两个动点的正中间时,A、B两点同时向数轴负方向运动,另一动点C和点B同时从点B位置出发向A运动,当遇到A后,立即返回向点B运动,遇到点B后又立即返回向点A运动,如此往返,直到B追上A时,C立即停止运动.若点C一直以20单位长度/s的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
参考答案:
【答案】(1)点A的运动速度是1个单位长度/s,点B的速度是4个单位长度/s;(2)点C行驶的路程是64个长度单位.
【解析】试题分析:
(1)设点A的运动速度为![]() 个单位长度/秒,则由题意可知,点B的运动速度为
个单位长度/秒,则由题意可知,点B的运动速度为![]() 个单位长度/秒,根据题意可得方程:
个单位长度/秒,根据题意可得方程: ![]() ,解此方程即可得到答案;
,解此方程即可得到答案;
(2)由(1)可知,点A在-3处,点B在12处,设![]() 秒后,原点在A、B两点中间,则由题意可得:
秒后,原点在A、B两点中间,则由题意可得: ![]() ,解此方程即可得到答案;
,解此方程即可得到答案;
(3)由题意可知,点C出发时,点A、B间相距![]() 个单位长度;要求点C的运动路程,只需求出点C的运动时间,即求出点B追上点A的时间即可,设点B在z秒后追上点A,则由题意可得:
个单位长度;要求点C的运动路程,只需求出点C的运动时间,即求出点B追上点A的时间即可,设点B在z秒后追上点A,则由题意可得: ![]() ,解此方程即可求得点C的运动时间,从而可求得点C的运动路程.
,解此方程即可求得点C的运动时间,从而可求得点C的运动路程.
试题解析:
(1)设点![]() 运动速度为
运动速度为![]() 个单位长度/s,则点
个单位长度/s,则点![]() 运动速度为
运动速度为![]() 个单位长度/s.
个单位长度/s.
由题意得![]() ,
,
解得![]() ,
,
所以点![]() 的运动速度是1个单位长度/s,点
的运动速度是1个单位长度/s,点![]() 的速度是4个单位长度/s;
的速度是4个单位长度/s;
出发3秒后,点A、B在数轴上的位置如图所示:
![]()
(2)设![]() s后,原点恰好处在
s后,原点恰好处在![]() 、
、![]() 的正中间.
的正中间.
由题意得![]()
解得![]()
即经过![]() s后,原点恰处在点
s后,原点恰处在点![]() 、
、![]() 的正中间;
的正中间;
(3)由题意可知,点C的运动时间就是点B追上点A所用时间,设![]() 追上
追上![]() 需时间
需时间![]() s
s
则![]() ,
,
解得![]() ,
,
所以![]() ,
,
即点![]() 运动的路程是64个长度单位.
运动的路程是64个长度单位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天,一蔬菜经营户用234元钱从蔬菜批发市场批了西红柿和茄子共50公斤到菜市场去卖,西红柿和茄子这天的批发价与零售价如下表所示:
品名
西红柿
茄子
批发价(单位:元 /公斤)
4.8
4.5
零售价(单位:元/公斤)
6
5.5
问:
(1)该经营户当天在蔬菜批发市场批了西红柿和茄子各多少公斤?
(2)他当天卖完这些西红柿和茄子能赚多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“2020年的6月21日是晴天”这个事件是( )
A.确定事件B.不可能事件C.必然事件D.不确定事件
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(﹣2019,2020)关于原点的对称点P′在( )
A.第一象限B.第二象限C.第三象限D.第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一棵树CD的10m高处的B点有两只猴子,它们都要到A处池塘边喝水,其中一只猴子沿树爬下走到离树20m处的池塘A处,另一只猴子爬到树顶D后直线跃入池塘的A处.如果两只猴子所经过的路程相等,试问这棵树多高?
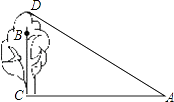
-
科目: 来源: 题型:
查看答案和解析>>【题目】南宁市是广西最大的罗非鱼养殖产区,被国家农业部列为罗非鱼养殖优势区域.某养殖场计划下半年养殖无公害标准化罗非鱼和草鱼,要求这两个品种总产量G(吨)满足:1 580≤G≤1 600,总产值为1 000万元.已知相关数据如表所示.
品种
单价(万元/吨)
罗非鱼
0.45
草鱼
0.85
求:该养殖场下半年罗非鱼的产量应控制在什么范围?(产值=产量×单价)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某加工厂九月份加工了10吨干果,十一月份加工了13吨干果.设该厂加工干果重量的月平均增长率为x,根据题意可列方程为 .
相关试题

