Question

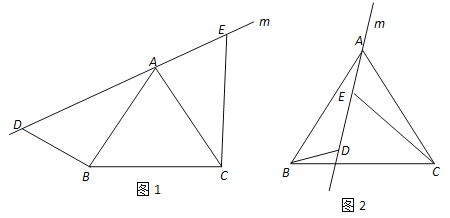
【题目】探索与证明：（1）如图1，直线m经过正三角形ABC的顶点A，在直线m上取两点 D，E，使得∠ADB=60°，∠AEC=60°．通过观察或测量，猜想线段BD，CE与DE之间满足的数量关系，并予以证明；

（2）将（1）中的直线m绕点A逆时针方向旋转一个角度到如图2的位置，并使∠ADB=120°，∠AEC=120°．通过观察或测量，请直接写出线段BD，CE与DE之间满足的数量关系．

Answer 1

【答案】(1)BD+CE=DE，证明见解析；（2）BD+DE=CE

【解析】试题分析：（1）通过证明△DAB≌△ECA（AAS），得出AD=CE，BD=AE，进而证得BD+CE= DE：

（2）通过△DAB≌△ECA（AAS），得出AD=CE，BD=AE，从而证得CE-BD=DE．

解：(1)猜想：BD+CE=DE.

证明：由已知条件可知：

∠DAB+∠CAE=120°,∠ECA+∠CAE=120°，

∴∠DAB=∠ECA.

在△DAB和△ECA中,

，

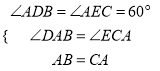∴△DAB≌△ECA(AAS).

∴AD=CE，BD=AE.

∴BD+CE=AE+AD=DE.

(2)猜想：CEBD=DE.

证明：由已知条件可知：

∠DAB+∠CAE=60°,∠ECA+∠CAE=60°，

∴∠DAB=∠ECA.

在△DAB和△ECA中,

，

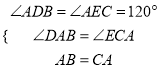∴△DAB≌△ECA(AAS).

∴AD=CE，BD=AE.

∴CEBD=ADAE=DE.