【题目】如图所示,在△ABC中,∠ABC与∠ACB的平分线交于点O,根据下列条件,求出∠BOC的度数.
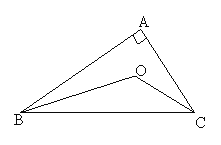
(1)已知∠ABC+∠ACB=100°,则∠BOC= .
(2)已知∠A=90°,求∠BOC的度数.
(3)从上述计算中,你能发现∠BOC与∠A的关系吗?请直接写出∠B0C与∠A的关系.
参考答案:
【答案】(1)1300;(2)1350;(3)∠BOC=900+![]() .
.
【解析】
试题(1)由已知求出∠OBC和∠OCB的和,即求出∠BOC;(2)由∠A求出∠ABC和∠ACB的和,由角平分线求出∠OBC和∠OCB的和,即求出∠BOC;(3)用三角形内角和定理和角平分线平分已知角导出∠BOC与∠A的关系.
试题解析:(1)∵∠ABC与∠ACB的平分线交于点O,∠ABC+∠ACB=100°,∴∠OBC+∠OCB=50,∴∠BOC=180-50=130.(2)∵∠A=90°,∴∠ABC+∠ACB=180-90=90,∵∠ABC与∠ACB的平分线交于点O,∴∠OBC+∠OCB=90÷2=45,∴∠BOC=180-45=135;(3)∠BOC=180-(∠OBC+∠OCB)=180-![]() (∠ABC+∠ACB)=180-
(∠ABC+∠ACB)=180-![]() (180-∠A)=180-90+
(180-∠A)=180-90+![]() ∠A=90+
∠A=90+![]() ∠A,即∠BOC=900+
∠A,即∠BOC=900+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=40°,分别以AB,AC为边作两个等腰三角形ABD和ACE,且AB=AD,AC=AE,∠BAD=∠CAE=90°.

(1)求∠DBC的度数.
(2)求证:BD=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的内容,再解决问题,
例题:若m2+2mn+2n2-6n+9=0,求m和n的值.
∵m2+2mn+2n2-6n+9=0
∴m2+2mn+n2+n2-6n+9=0
∴(m+n)2+(n-3)2=0
∴m+n=0,n-3=0
∴m=-3,n=3
问题(1)若x2+2y2-2xy-4y+4=0,求xy的值.
(2)已知a,b,c是△ABC的三边长,满足a2+b2-6a-6b+18+| 3-c |=0,请问△ABC是怎样形状的三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式x2-4y2-2x+4y,细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式,过程为:x2-4y2-2x+4y=(x+2y)(x-2y)-2(x-2y)=(x-2y)(x+2y-2).这种分解因式的方法叫分组分解法,利用这种方法解决下列问题:
(1)分解因式:a2-4a-b2+4;
(2)若△ABC三边a、b、c满足a2-ab-ac+bc=0,试判断△ABC的形状.
-
科目: 来源: 题型:
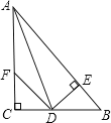
查看答案和解析>>【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
证明:(1)CF=EB.
(2)AB=AF+2EB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的对角线相交于点O,过点O的任意一条直线与边AD相交于点E,与边BC相交于点F,求证:OE=OF.

相关试题

