【题目】已知边长为3的正方形ABCD中,点E在射线BC上,且BE=2CE,连结AE交射线DC于点F,将△ABE沿直线AE翻折,点B落在点B1处.

(1)如图1,若点E在线段BC上,求CF的长;
(2)求sin∠DAB1的值.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]() .
.
【解析】
试题分析:(1)利用平行线性质以及线段比求出CF的值;
(2)本题要分两种方法讨论:①若点E在线段BC上;②若点E在边BC的延长线上.需运用勾股定理求出与之相联的线段;
试题解析:(1)∵AB∥DF,
∴![]() ,
,
∵BE=2CE,AB=3,
∴![]() ,
,
∴CF=![]() ;
;
(2)①若点E在线段BC上,如图1,设直线AB1与DC相交于点M.
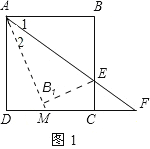
由题意翻折得:∠1=∠2.
∵AB∥DF,
∴∠1=∠F,
∴∠2=∠F,
∴AM=MF.
设DM=x,则CM=3-x.
又∵CF=1.5,
∴AM=MF=![]() -x,
-x,
在Rt△ADM中,AD2+DM2=AM2,
∴32+x2=(![]() -x)2,
-x)2,
∴x=![]()
∴DM=![]() ,AM=
,AM=![]() ,
,
∴sin∠DAB1=![]() ;
;
②若点E在边BC的延长线上,如图2,设直线AB1与CD延长线相交于点N.
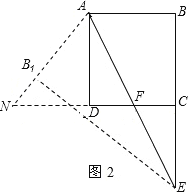
同理可得:AN=NF.
∵BE=2CE,
∴BC=CE=AD.
∵AD∥BE,
∴![]() ,
,
∴DF=FC=![]() ,
,
设DN=x,则AN=NF=x+![]() .
.
在Rt△ADN中,AD2+DN2=AN2,
∴32+x2=(x+![]() )2,
)2,
∴x=![]() .
.
∴DN=![]() ,AN=
,AN=![]()
sin∠DAB1=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年7月23日,记者从省旅发委获悉,上半年我省实现旅游总收入约2381亿元人民币,该数据用科学记数法表示为( )
A. 2.381×1011元 B. 2.381×1012元 C. 0.2381×1012元 D. 23.81×1010元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
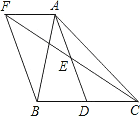
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
-
科目: 来源: 题型:
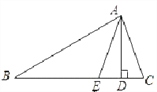
查看答案和解析>>【题目】△ABC中,AD⊥BC,AE平分∠BAC交BC于点E.
(1)∠B=30°,∠C=70°,求∠EAD的大小;
(2)若∠B<∠C,则2∠EAD与∠C-∠B是否相等?若相等,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=-x2+bx+c与x轴交于A、B两点,且B点的坐标为(3,0),经过A点的直线交抛物线于点D (2, 3).
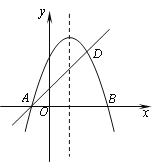
(1)求抛物线的解析式和直线AD的解析式;
(2)过x轴上的点E (a,0) 作直线EF∥AD,交抛物线于点F,是否存在实数a,使得以A、D、E、F为顶点的四边形是平行四边形?如果存在,求出满足条件的a;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证:四边形DEBF是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有( )个
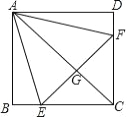
A. 4 B. 3 C. 2 D. 1
相关试题

