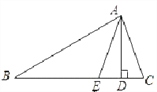
【题目】△ABC中,AD⊥BC,AE平分∠BAC交BC于点E.
(1)∠B=30°,∠C=70°,求∠EAD的大小;
(2)若∠B<∠C,则2∠EAD与∠C-∠B是否相等?若相等,请说明理由.
参考答案:
【答案】(1)∠EAD=20°;(2)2∠EAD=∠C∠B,理由见解析.
【解析】分析:(1)由三角形内角和定理可求得∠BAC的度数,在Rt△ADC中,可求得∠DAC的度数,AE是角平分线,有∠EAC=![]() ∠BAC,故∠EAD=∠EAC-∠DAC;(2)由(1)知,用∠C和∠B表示出∠EAD,即可知2∠EAD与∠C-∠B的关系.
∠BAC,故∠EAD=∠EAC-∠DAC;(2)由(1)知,用∠C和∠B表示出∠EAD,即可知2∠EAD与∠C-∠B的关系.
本题解析:
(1)∵∠B=30°,∠C=70°,∴∠BAC=180°﹣∠B﹣∠C=80°,
∵AE是角平分线,∴ ∠EAC=![]() ∠BAC=40°,∵AD是高,∠C=70°,
∠BAC=40°,∵AD是高,∠C=70°,
∴∠DAC=90°﹣∠C=20°,∴∠EAD=∠EAC﹣∠DAC=40°﹣20°=20°;
(2)由(1)知,∠EAD=∠EAC﹣∠DAC=![]() ∠BAC﹣(90°﹣∠C)①,
∠BAC﹣(90°﹣∠C)①,
把∠BAC=180°﹣∠B﹣∠C代入①,整理得∠EAD=![]() ∠C﹣
∠C﹣![]() ∠B,
∠B,
∴2∠EAD=∠C﹣∠B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. ﹣2﹣3=﹣1 B. (﹣2)3=﹣6 C. ﹣2+3=1 D. (﹣21)÷7=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年7月23日,记者从省旅发委获悉,上半年我省实现旅游总收入约2381亿元人民币,该数据用科学记数法表示为( )
A. 2.381×1011元 B. 2.381×1012元 C. 0.2381×1012元 D. 23.81×1010元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
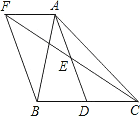
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知边长为3的正方形ABCD中,点E在射线BC上,且BE=2CE,连结AE交射线DC于点F,将△ABE沿直线AE翻折,点B落在点B1处.

(1)如图1,若点E在线段BC上,求CF的长;
(2)求sin∠DAB1的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=-x2+bx+c与x轴交于A、B两点,且B点的坐标为(3,0),经过A点的直线交抛物线于点D (2, 3).
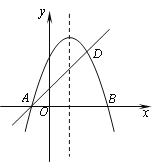
(1)求抛物线的解析式和直线AD的解析式;
(2)过x轴上的点E (a,0) 作直线EF∥AD,交抛物线于点F,是否存在实数a,使得以A、D、E、F为顶点的四边形是平行四边形?如果存在,求出满足条件的a;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证:四边形DEBF是菱形.

相关试题

