【题目】在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F
（1）求证：△AEF≌△DEB；
（2）证明：四边形ADCF是菱形；
（3）若AB=4，AC=5，求菱形ADCF的面积．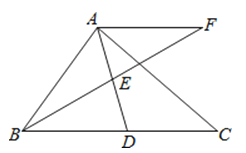

参考答案：

【答案】（1）证明：∵AF∥BD，
∴∠AFE=∠DBE，
∵E是AD中点，
∴AE=ED，
在△BDE和△FAE中，
，
∴△AFE≌△DBE．
（2）证明：连接CF．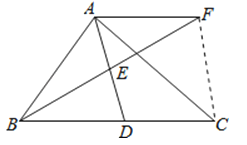

∵△AFE≌△DBE，
∴AF=BD
∵∠BAC=90°，BD=CD，
∴AD=DC=DB，
∴AF∥CD，AF=DC，
∴四边形ADCF是平行四边形，
∵DA=CD，
∴四边形ADCF是菱形．
（3）∵S△ABC=×AB×AC=10，
∵四边形ADCF是菱形，BD=DC，S△ABC=2S△ADC ，
∴S菱形ADCF=2S△ADC=10．
【解析】（1）根据AAS证明即可判定．
（2）先证明四边形ADCF是平行四边形，再证明DA=DC即可．
（3）利用S菱形ADCF=2S△ADC=S△ABC即可求解．

关闭