【题目】已知反比例函数y= ![]() (k为常数,k≠0)的图象经过点A(2,3).
(k为常数,k≠0)的图象经过点A(2,3).
(Ⅰ)求这个函数的解析式;
(Ⅱ)判断点B(﹣1,6),C(3,2)是否在这个函数的图象上,并说明理由;
(Ⅲ)当﹣3<x<﹣1时,求y的取值范围.
参考答案:
【答案】解:(Ⅰ)∵反比例函数y=![]() (k为常数,k≠0)的图象经过点A(2,3),
(k为常数,k≠0)的图象经过点A(2,3),
∴把点A的坐标代入解析式,得
3=![]() ,
,
解得,k=6,
∴这个函数的解析式为:y=![]() ;
;
(Ⅱ)∵反比例函数解析式y=![]() ,
,
∴6=xy.
分别把点B、C的坐标代入,得
(﹣1)×6=﹣6≠6,则点B不在该函数图象上.
3×2=6,则点C在该函数图象上;
(Ⅲ)∵当x=﹣3时,y=﹣2,当x=﹣1时,y=﹣6,
又∵k>0,
∴当x<0时,y随x的增大而减小,
∴当﹣3<x<﹣1时,﹣6<y<﹣2.
【解析】(1)把点A的坐标代入已知函数解析式,通过方程即可求得k的值.
(Ⅱ)只要把点B、C的坐标分别代入函数解析式,横纵坐标坐标之积等于6时,即该点在函数图象上;
(Ⅲ)根据反比例函数图象的增减性解答问题.
【考点精析】通过灵活运用反比例函数的性质,掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若新规定这样一种运算法则:a※b=a2+2ab,例如3※(﹣2)=32+2×3×(﹣2)=﹣3.
(1)试求(﹣2)※3的值;
(2)若(﹣5)※x=﹣2﹣x,求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于点O成中心对称的两个四边形ABCD和DEFG,AD、BE、CF、DG都过______
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(-1)×(-2)的结果是( )
A. 2. B. 1. C. -2. D. -3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F
(1)求证:△AEF≌△DEB;
(2)证明:四边形ADCF是菱形;
(3)若AB=4,AC=5,求菱形ADCF的面积.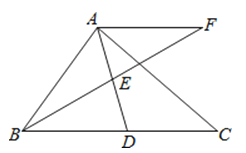
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(1,a)、点B(b,2)关于原点对称,则a+b的值为 .
相关试题

