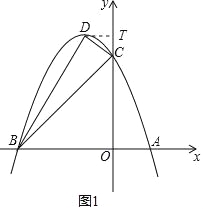
【题目】如图,抛物线y=![]() +bx+c的对称轴为x=﹣1,该抛物线与x轴交于A、B两点,且A点坐标为(1,0),交y轴于C(0,3),设抛物线的顶点为D.
+bx+c的对称轴为x=﹣1,该抛物线与x轴交于A、B两点,且A点坐标为(1,0),交y轴于C(0,3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标.
(2)试判断△BCD的形状,并予证明.
(3)在对称轴上是否存在一点P,使得△ACP为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)y=![]() ﹣2x+3,顶点D为(﹣1,4);(2)△DCB为直角三角形,理由详见解析;(3) 存在满足条件的点P,其坐标为(﹣1,1)或(﹣1,
﹣2x+3,顶点D为(﹣1,4);(2)△DCB为直角三角形,理由详见解析;(3) 存在满足条件的点P,其坐标为(﹣1,1)或(﹣1,![]() )或(﹣1,
)或(﹣1,![]() )或(﹣1,0)或(﹣1,6).
)或(﹣1,0)或(﹣1,6).
【解析】
试题分析:(1)根据抛物线的对称性得到点B的坐标为(﹣3,0),故设抛物线为两点式方程y=a(x﹣1)(x+3),把点C的坐标代入即可求得a的值;利用配方法将抛物线解析式转化为顶点式,即可得到顶点D的坐标;
(2)过D作DT⊥y轴于T,则可求得∠DCT=45°,∠BCO=45°,则可判断△BCD的形状;
(3)可设出P(﹣1,t),则可分别表示出AP、CP、AC的长度,分AP=CP、AP=AC和CP=AC三种情况分别可得到关于t的方程,可求得P点坐标.
试题解析:(1)点A(1,0)关于x=﹣1的对称点B(﹣3,0),
设过A(1,0)、B(﹣3,0)的抛物线为y=a(x﹣1)(x+3),
该抛物线又过C(0,3),则有:3=﹣3a,解得a=﹣1,
即y=![]() =
=![]() ﹣2x+3,顶点D为(﹣1,4);
﹣2x+3,顶点D为(﹣1,4);
(2)△DCB为直角三角形,理由如下:
过D点,作DT⊥y轴于T,如图1,
则T(0,4).
∵DT=TC=1,
∴△DTC为等腰直角三角形,
∴∠DCT=45°,
同理可证∠BCO=45°,
∴∠DCB=90°,
∴△DCB为直角三角形;
(3)设P(﹣1,t),
∵A(1,0),C(0,3),
∴![]() =
=![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,![]() =
=![]() =10,
=10,
∵△APC为等腰三角形,
∴有AP=CP、AP=AC和CP=AC三种情况,
①当AP=CP时,则有![]() =
=![]() ,即
,即![]() =
=![]() ,解得t=1,此时P(﹣1,1);
,解得t=1,此时P(﹣1,1);
②当AP=AC时,则有![]() =
=![]() ,即
,即![]() =10,解得t=
=10,解得t=![]() ,此时P(﹣1,
,此时P(﹣1,![]() )或(﹣1,
)或(﹣1,![]() );
);
③当CP=AC时,则有![]() =
=![]() ,即
,即![]() =10,解得t=0或t=6,此时P(﹣1,0)或P(﹣1,6);
=10,解得t=0或t=6,此时P(﹣1,0)或P(﹣1,6);
综上可知存在满足条件的点P,其坐标为(﹣1,1)或(﹣1,![]() )或(﹣1,
)或(﹣1,![]() )或(﹣1,0)或(﹣1,6).
)或(﹣1,0)或(﹣1,6).
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的两边分别为4和6,则这个三角形的周长是 ( )
A. 14 B. 16 C. 24 D. 14或16
-
科目: 来源: 题型:
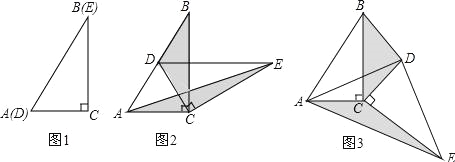
查看答案和解析>>【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=α,若固定△ABC,将△DEC绕点C旋转.
(1)当△DEC绕点C旋转到点D恰好落在AB边上时,如图2,则此时旋转角为 (用含的式子表示).
(2)当△DEC绕点C旋转到如图3所示的位置时,小杨同学猜想:△BDC的面积与△AEC的面积相等,试判断小杨同学的猜想是否正确,若正确,请你证明小杨同学的猜想.若不正确,请说明理由.
-
科目: 来源: 题型:
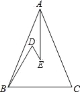
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AE平分∠BAC,∠D=∠DBC=60°,若BD=5cm,DE=3cm,则BC的长是 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.|﹣2|=﹣2
B.a2?a3=a6
C.(﹣3)﹣2=
D.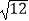 =
=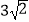
-
科目: 来源: 题型:
查看答案和解析>>【题目】若干本书分给某班同学,如果每人6本,则余18本;如果每人7本,则缺24本,这个班的学生有___人,书有____本.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学竞赛共有20道题,答对一题得5分,不答或答错一题扣3分,若要得到84分,则需要答对几道题?设答对x道题,可列方程为________.
相关试题

